Incoherent scatter radar (ISR) observations of high-frequency enhanced ion and plasma lines induced by X/O mode pumping around the critical altitude

1.   Introduction

A powerful ground-based Incoherent Scatter Radar (ISR) installation can measure various properties of the ionosphere plasma, such as electron temperature, electron density, ion temperature, and ion velocity. A great variety of phenomena, excited by powerful radio waves in ordinary polarization mode (O mode), are regularly observed by ISR; among these phenomena are large scale enhancement in electron temperature (Gordon and Carlson, 1974; Meltz et al., 1974; Mantas et al., 1981; Jones et al., 1986; Robinson, 1989; Gurevich, 2007) and the high-frequency enhanced ion line (HFIL) and plasma line (HFPL) (Carlson et al., 1972; Showen and Kim,1978; Morales et al., 1982; Hagfors et al., 1983; Duncan,1985; Djuth et al., 1986; Robinson, 1989; Gurevich, 2007). Especially, the HFIL and HFPL can be observed in ISR spectra, and the large scale enhancement in electron temperature can be detected by standard analysis of ISR spectra. It should be noted that due to the lower reflecting altitude of energy pumped via the extraordinarily polarized mode (X mode), appreciable enhancement of the HFIL and HFPL should be unexpected in ISR observations when X mode pumping is employed (Gordon and Carlson, 1974; Meltz et al., 1974; Robinson, 1989; Gurevich, 2007).

Recently, however, Wang et al. (Wang X et al., 2016a, b, 2018; Wang X and Zhou C, 2017) and Feng T et al. (2020) claimed that some effects similar to those excited by the O mode pumping were excited by the X mode pumping at the European Incoherent Scatter Scientific Association (EISCAT) facility. Wang X et al. (2016a) proposed that a small parallel component of the X mode pumping might satisfy the threshold of parametric decay instability (PDI) in an inhomogeneous plasma, and that a modified kinetic electron distribution might satisfy the PDI frequency matching condition. Further, a simulation demonstrated that a small parallel component of an X mode pumping can be present in the inhomogeneous ionosphere (Wang X et al., 2016b). Wang X and Zhou C (2017) also proposed that the HFIL and HFPL demonstrated a dependence on incidence angle of the X mode pumping, and provided evidence of a non-Maxwellian distribution in the heated region. Blagoveshchenskaya et al. (2020) claimed that there is not an adequate theory describing interactions between the X mode pumping and the ionosphere. Indeed, debates continue over the HFIL and HFPL excited by the X mode pumping (Wang X et al., 2016b, 2018；Blagoveshchenskaya et al., 2020; Li ZY et al., 2021). In this study, the initial behavior of the HFIL is investigated by examining the ISR spectra, electron temperature, and ionosphere conditions around the critical altitude.

2.   Experiment and Measurement

A campaign involving the EISCAT heater and ultra high frequency (UHF) ISR was conducted on 21 Feb. 2013, described in more detail by Wang X et al. (2016b). In brief, the heater and ISR were pointed in the geomagnetic field-aligned direction. With a heating cycle of 10 mins on and 5 mins off, alternating O/X mode pumping was performed at the frequencies ${f_{{\text{HF}}}} = 7.1{\text{ MHz}}$ from 12:01 to 14:26 UT, and ${f_{{\text{HF}}}} = 5.423{\text{ MHz}}$ from 14:31 to 15:41 UT. It is important to note that ${f_{{\text{HF}}}}$ is intended to be near the critical frequency. Unfortunately, the critical frequencies ${f_{\text{0}}}{{\text{F}}_2}$ and ${f_{\text{x}}}{{\text{F}}_2}$ were not quiet; in general, they trended downward during the experiment. Sharp drops or rises in ${f_{\text{0}}}{{\text{F}}_2}$ and ${f_{\text{x}}}{{\text{F}}_2}$ took place at 12:24, 12:40, 13:18, 14:12 and 14:54 UT, as shown in Figure 1. As a typical case, we focus here on the measurement from 12:16 to 15:11 UT.

Figure  1.  Example of the evolution of the critical frequency during the experiment; ${f_{\text{0}}}{{\text{F}}_2}$ was recorded in ionosonde with a time resolution of 2 mins, and ${f_{\text{x}}}{{\text{F}}_2} \approx \dfrac{1}{2}{f_{{\text{ce}}}} + {f_0}{{\text{F}}_2}$, where the electron gyrofrequency ${f_{{\text{ce}}}} \approx 1.34\;{\text{MHz}}$ (Wu J et al., 2017).

DownLoad: Full-Size Img PowerPoint

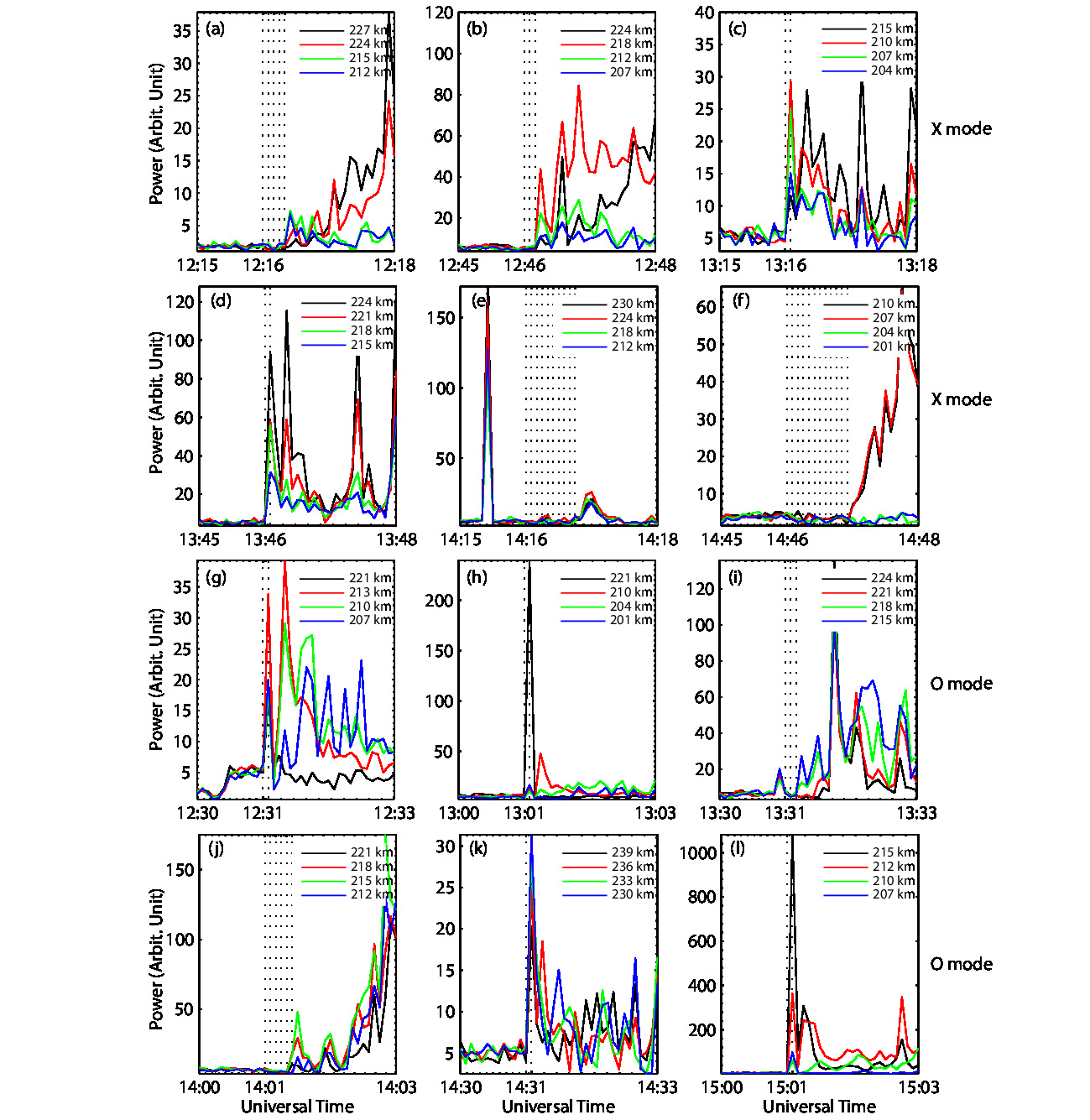
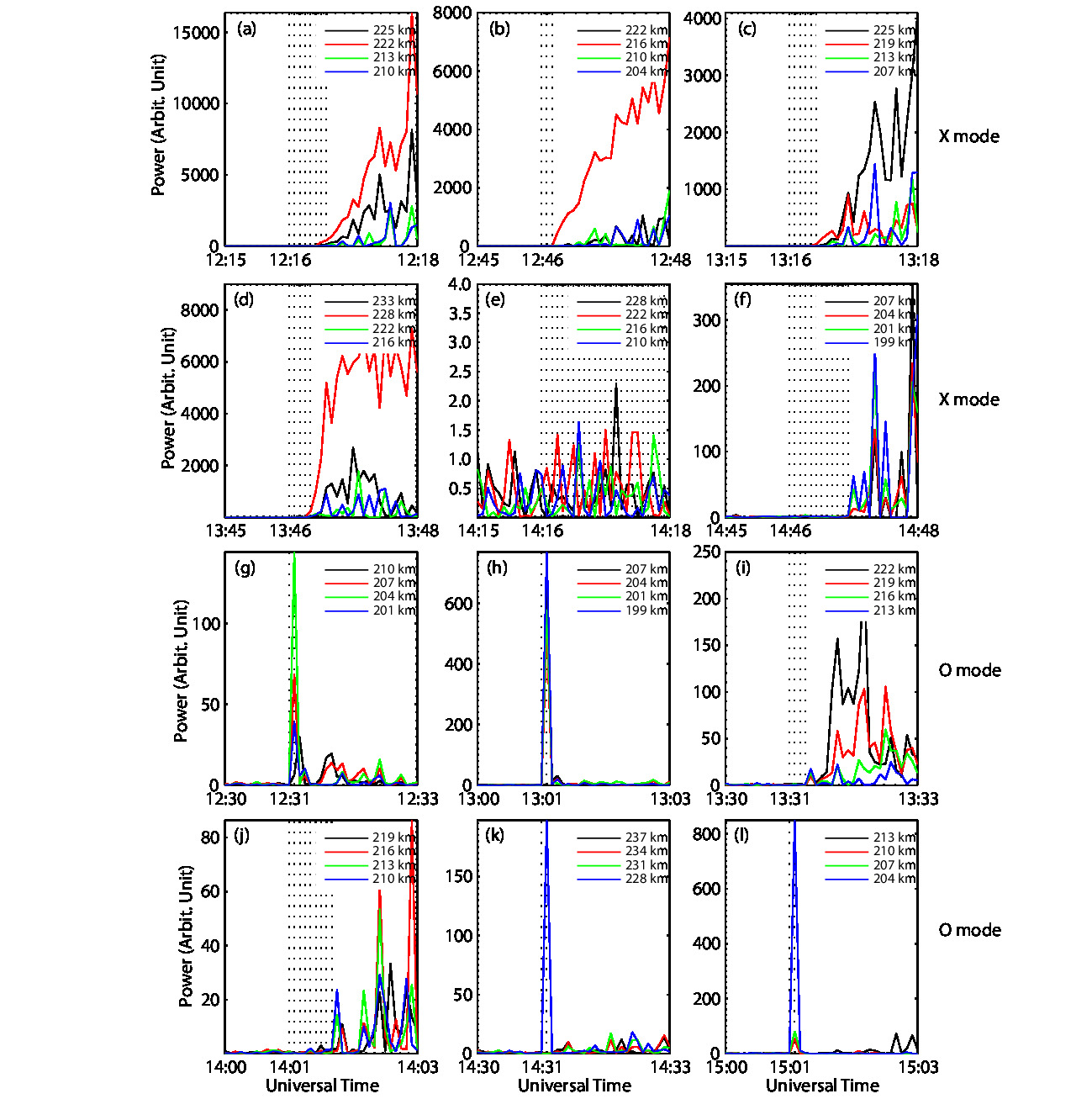
Figure 2 demonstrates the power of those ion lines in the last one minute before the pumping onset and in the first two minutes after the pumping onset. One can see that the HFIL is delayed by ~10–55 s after the pumping onset at 12:16, 12:46, 13:31, 14:01, 14:16 and 14:46 UT, whereas it appears immediately after pumping onset in the remaining heating cycles. Note that the delay of the HFIL has not shown an obvious dependence on the pumping mode, although the HFIL is delayed more frequently in the X mode pumping than in the O mode pumping. In Figure 3, all of the observed HFPL are delayed for a longer time than the corresponding HFIL except those at 12:31, 13:01, 14:31 and 15:01 UT.

Figure  2.  The initial evolution of ion line power at some altitudes, obtained through 5 s integration in the frequency range from −18 to 18 kHz by considering the PDI timescale of the order of milliseconds (Robinson, 1989; Gurevich, 2007).

DownLoad: Full-Size Img PowerPoint

Figure  3.  The same as Figure 2, but for plasma line, where (a)–(e) and (g)–(j) are integrated in the frequency range of 7–7.2 MHz, and (f), (k) and (i) are integrated in the frequency range of 5.323–5.523 MHz.

DownLoad: Full-Size Img PowerPoint

Figure 4 illustrates the electron temperature ${T_{\text{e}}}$ in the altitude range of ~150–350 km. It is evident that ${T_{\text{e}}}$ is not significantly enhanced within 10 s after the pumping onset at 12:16, 12:46, 13:31, 14:01, 14:16 and 14:46 UT, whereas it is enhanced in the remaining heating cycles. It is interesting to note that the initial evolution of ${T_{\text{e}}}$ is temporally consistent with that of the ion line power shown in Figure 2, and has not shown any obvious dependence on the pumping mode. Furthermore, ${T_{\text{e}}}$ is enhanced in ~20 s after pumping onset in all of the cycles except those at 14:01 and 14:46 UT.

Figure  4.  The initial evolution of ${T_{\text{e}}}$.

DownLoad: Full-Size Img PowerPoint

Figure 5 illustrates an example of some ion and plasma lines at 12:16:00, 12:16:20, 12:16:40, 12:17:00, 12:17:20, 12:17:40 and 12:18:00 UT at several altitudes. As might be expected, the ion and plasma lines are not enhanced at 12:16:00 UT. The HFILs of ~11.9 and ~13.1 kHz are observed in the time interval of 12:16:20–2:18:00 UT at altitude ~215 km. At altitude ~227 km, the HFILs of ~9.5 and ~11.9 kHz are seen, respectively, at 12:16:20 and 12:16:40 UT, and the HFIL of ~10.71 kHz appears in the time interval of 12:17:00–12:18:00 UT. Furthermore, no obvious HFPL is detected at altitude ~213 km, whereas at altitude ~225 km, an HFPL of ~−7.091 MHz appears at 12:16:40 UT, and HFPL of ~−7.089 MHz appears at 12:17:00–12:18:00 UT.

Figure  5.  The ion and plasma lines in the time interval of 12:16:00–12:18:00 UT, obtained by integrating over a period of 20 s for the sake of line smoothing.

DownLoad: Full-Size Img PowerPoint

3.   Discussion

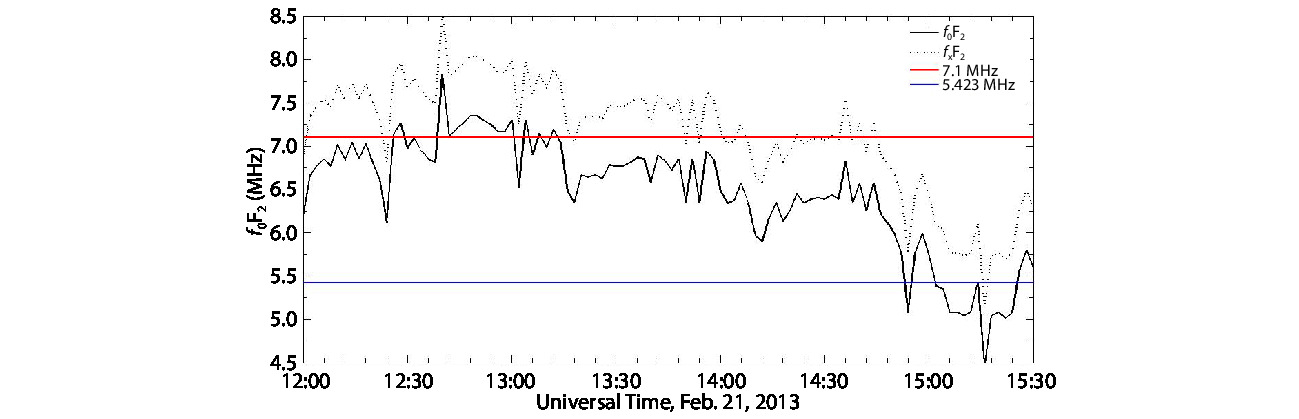
As demonstrated in Figures 2 and 3, not only the X mode pumping but also the O mode pumping excites the HFIL and HFPL; delays are observed in both cases. The possibility of leakage of the X mode pumping to the O mode pumping may not be ignored for the following reasons. (1) In reality, the EISCAT heater cannot perfectly separate the O mode pumping from the X mode pumping, so leakage of X mode pumping energy to the O mode should be expected (Blagoveshchenskaya et al., 2014). (2) Moreover, in the typical ionosphere the O mode has a low PDI threshold (of ~17–35 MW) (Robinson, 1989; Bryers et al., 2013), which may be satisfied by leakage of the high power X-mode-pumped energy to the O mode. (3) Using the model NEC2 (Numerical Electromagnics Code), it is estimated that the leakage from X mode pumping to the O mode can satisfy the threshold of PDI (Li ZY et al., 2021). (4) The model developed by Senior et al. (2011) estimates leakage of the X mode pumping to the O mode as ~2.3–5 MW , but one should be aware that the gain pattern of the EISCAT heater is modeled by assuming a perfectly reflecting ground (Senior et al., 2011), and that the side lobe of the gain pattern may be unreliable. As a matter of fact, the ground at EISCAT in Tromsø is not a perfect reflector, but is composed of soil, dry sand, gravel, fine sediment and rock (Senior et al., 2011). (5) During the experiment, the ionosphere was quite active, implying that the critical frequency should be expected to be fluctuating, but the O/X mode pumpings were both operated at constant frequencies during the experiment; that is, at 7.1 MHz from 12:01 to 14:26 UT and at 5.423 MHz from 14:31 to 15:41 UT. Thus, spatiotemporal uncertainties, such as changing profiles of ion mass and electron density due to active convection at the critical altitude, may have made the ionosphere over-dense, and thus affected excitement of the PDI at the critical altitude.

The lack of the Bragg condition for the enhanced acoustic wave may have led to the disappearance of the HFIL. In the case of backscattering, the ISR can only observe an ion acoustic wave that satisfies the Bragg condition

where ${k_{{\text{ia}}}}$ and ${k_{\text{r}}}$ denote the wave number of an ion acoustic wave and the wave number of radar, respectively. ${k_{{\text{ia}}}}$ follows the dispersion function:

where ${\omega _{{\text{ia}}}}$, $\gamma$, ${K_{\text{B}}}$, and ${m_{\text{i}}}$ are, respectively, the frequency of ion acoustic wave, the adiabatic index, the Boltzmann constant, and the effective ion mass. (Baumjohann and Treumann, 1996). Having stated the above theoretical relation, the impact of ${T_{\text{e}}}$ on the delay of the HFIL will be examined in the following.

By comparing Figure 2 with Figure 4, one can find a spatiotemporally positive correlation between the delay of the HFIL and the delay of the enhanced ${T_{\text{e}}}$, as demonstrated in Figures 6a and 6b. In the time interval of 12:16–13:46 UT, the HFIL delay of ~10–20 s corresponds temporally to the $\Delta {T_{\text{e}}}$ delay of ~20 s, and the immediate HFIL corresponds temporally to the immediate $\Delta {T_{\text{e}}}$. After 13:46 UT, the above behavior still holds, but the HFIL is delayed by ~25–55 s and $\Delta {T_{\text{e}}}$ is delayed by ~25–120 s. This may be due to the severe jitter of ${f_{\text{0}}}{{\text{F}}_2}$ and ${f_{\text{x}}}{{\text{F}}_2}$ in the time intervals of 14:00–14:20 UT and 14:46–15:00 UT, as shown in Figure 1. Indeed, the measurement of ${f_{\text{0}}}{{\text{F}}_2}$ by ionosonde is rough, but the ionospheric trend should be available. Moreover, Figures 6b and 6c demonstrate that at altitude ~200 km there is a negative correlation between $\Delta T{}_{{\text{e10}}}$ and the delay of $\Delta {T_{\text{e}}}$, which simply implies that when $\Delta {T_{\text{e}}}$ is delayed by ~20 s and more after the pumping onset, ${T_{\text{e}}}$ will not be enhanced in 10 s after the pumping onset.

Figure  6.  (a) The delay of the HFIL given by Figure 2, (b) the delay of the enhanced ${T_{\text{e}}}$ given by Figure 4, (c) $\Delta {T_{{\text{e10}}}} = T{}_{{\text{e10}}} - T{}_{{\text{e0}}}$ at altitude ~200 km and (d) ${k_{{\text{ia}}}} - 2{k_{\text{r}}}$, where ${k_{{\text{ia}}}} = \sqrt {\dfrac{{\omega _{{\text{ia}}}^{\text{2}}{m_{\text{i}}}}}{{\gamma {K_{\text{B}}}{T_{{\text{e10}}}}}}}$, ${k_{\text{r}}} = 19.5{\text{ }}{{\text{m}}^{ - 1}}$ for UHF radar at EISCAT, $T{}_{{\text{e0}}}$ denotes the immediate electron temperature when the pumping is turned on, and $T{}_{{\text{e10}}}$ denotes the electron temperature 10 s after the onset of pumping, both of which are given by Figure 4. For the sake of computational simplicity, (1) ${f_{{\text{ia}}}} = 9.624{\text{ kHz}}$ is considered to be the typical frequency of the HFIL during the experiment (Wang X et al., 2016b, Figure 3); (2) the effective ion mass is computed by ${m_{\text{i}}} = \dfrac{{{N_{{{\text{O}}^{+}}}}}}{{{N_{\text{e}}}}}{m_{{\text{i}}{{\text{O}}^ + }}} + \left( {1 - \dfrac{{{N_{{{\text{O}}^{+}}}}}}{{{N_{\text{e}}}}}} \right){m_{{\text{iO}}_2^ + }}$, where ${m_{{\text{i}}{{\text{O}}^ + }}}$ and ${m_{{\text{iO}}_2^ + }}$ denote oxygen atom mass and oxygen molecule mass, and the density ratio of ${{\text{O}}^ + }$ to electron $\dfrac{{{N_{{{\text{O}}^{+}}}}}}{{{N_{\text{e}}}}}$ is obtained from the International Reference Ionosphere 2007; (3) due to ${m_{{\text{iO}}_2^ + }} \approx {m_{{\text{iN}}{{\text{O}}^{\text{ + }}}}}$, ${\text{O}}_2^ +$ and ${\text{N}}{{\text{O}}^ + }$ are considered together.

DownLoad: Full-Size Img PowerPoint

Next, ${k_{{\text{ia}}}}$ can be obtained and then used to determine whether the Bragg condition was satisfied during the initial evolution, as shown in Figure 6d. At 12:16, 12:46, 13:31, 14:01, 14:16 and 14:46 UT, ${T_{\text{e}}}$ is not significantly enhanced in the first 10 s after pumping begins; then ${k_{{\text{ia}}}} - 2{k_{\text{r}}}$ is successively ~10.6, ~17, ~15.7, ~17.4, ~18.3 and ~22 m^-1 , all of which significantly deviate from zero. Namely, ${k_{{\text{ia}}}}$ does not significantly satisfy ${k_{{\text{ia}}}} = 2{k_{\text{r}}}$ and the HFIL should not be observed by the ISR. Otherwise, at 12:31, 13:01, 13:16, 13:46, 14:31 and 15:01 UT, ${T_{\text{e}}}$ was significantly enhanced (up to ~2500–5000 K) in the first 10 s after the pumping onset; in those cases, ${k_{{\text{ia}}}} - 2{k_{\text{r}}}$ was successively ~−6.8, ~2.8, ~2.4, ~7.4, ~−3.8, and ~−7.7 m^-1, which deviate only slightly from zero. In other words, ${k_{{\text{ia}}}}$ does approximately satisfy the Bragg condition and the ISR was able to observe those enhanced ion acoustic waves, which, indeed, within a small range of ${k_{{\text{ia}}}}$, may have contributed to the HFIL. In addition, when $\Delta {T_{{\text{e10}}}} \approx$~2000 K at 13:01, 13:16 and 13:46 UT, ${k_{{\text{ia}}}} - 2{k_{\text{r}}}$ positively approached zero, whereas ${k_{{\text{ia}}}} - 2{k_{\text{r}}}$ negatively approaches zero when $\Delta {T_{{\text{e10}}}} >$~3800 K at 12:31, 14:31 and 15:01 UT. This implies that, in the present case, when $\Delta {T_{{\text{e10}}}} \approx 2800{\text{ K}}$, ${k_{{\text{ia}}}} - 2{k_{\text{r}}} \approx 0$, namely, the Bragg condition, was exactly satisfied. This seems to imply that the interaction between the pumping and ionosphere may have taken place during the initial evolution, but the HFIL was not observed due to the lack of ${k_{{\text{ia}}}} \approx 2{k_{\text{r}}}$ at 12:16, 12:46, 13:31, 14:01, 14:16, and 14:46 UT.

Besides the impact of ${T_{\text{e}}}$ on the traveling path, the HFIL may not have been observed due to a variety of spatiotemporal uncertainties, such as strong convection, as well as changes in the profiles of ion mass and electron density at the critical altitude, which may have had a significant impact on the traveling path of the enhanced ion acoustic and Langmuir waves so that the Bragg condition was not satisfied. In those over-dense conditions at 12:16 and 14:46 UT, the sharp decrease of ~1 MHz in the critical frequency implies that the ionosphere should have been intensely active and that the ion profile may have been significantly modified, thus the non-observation of the HFIL was probably due to failure of the Bragg condition. At 15:01 UT, however, a sharp decrease of ~1 MHz in the critical frequency took place, but the HFIL was not delayed. Moreover, comparison of Figures 2 and 3 reveals that the HFPL time delay was different from that of the corresponding HFIL; for instance, the HFPL by ~20 s and the HFPL by ~35 s at 12:16 UT, which is not consistent with typical experimental results (Robinson, 1989). Enhanced ion acoustic and Langmuir waves are usually induced simultaneously by the PDI, on a timescale of the order of milliseconds (Robinson, 1989; Gurevich, 2007). Observations imply that the Bragg conditions of the enhanced ion acoustic and Langmuir waves are not simultaneously satisfied on their traveling paths.

Nevertheless, it cannot be ruled out that the PDI was not excited in the initial evolution. For example, ion and plasma lines in the time interval of 12:16:00–12:18:00 UT are examined, as illustrated in Figure 5. As expected, those ion and plasma lines are not enhanced at 12:16:00 UT. In the time interval of 12:16:20–12:18:00 UT, the HFIL of ~11.9 kHz appears at altitude ~212 km, whereas no obvious HFPL is found at altitude ~213 km. A possible explanation is that, during this period, the HFIL may not have been excited by the pumping, but the natural ion acoustic wave at 11.9 kHz may have satisfied the Bragg condition due to the enhanced ${T_{\text{e}}}$ on the traveling path. Here the natural ion acoustic wave denotes those not enhanced by the pumping. Indeed, the natural ion acoustic wave covers a wide frequency spectrum, due to the wide spectrum of ion mass distribution in ionosphere. Considering ${f_{{\text{ia}}}} = 11.9{\text{ kHz}}$, ${T_{\text{e}}} \approx 3200{\text{ K}}$, and ${m_{\text{i}}} = 3.72 \times {10^{ - 26}}{\text{ kg}}$ computed as in Figure 6, thus ${k_{{\text{ia}}}} \approx 39.6{\text{ }}{{\text{m}}^{ - 1}}$. In other word, when ${T_{\text{e}}} \approx 3200{\text{ K}}$, the natural ion line of 11.9 kHz should be observed by the ISR. Further, in the time interval of 12:17:00–12:18:00 UT, it is evident that the HFIL of 10.71 kHz was observed at altitude ~227 km, which is an exact match for the HFPL of 7.089 MHz observed at altitude ~225 km, as indicated by the matching frequency ${f_{{\text{HF}}}} = {f_{\text{L}}} + {f_{{\text{ia}}}}$, where ${f_{\text{L}}}$ is the HFPL frequency. The above analysis implies that, due to the enhanced ${T_{\text{e}}}$ on the traveling path, the natural ion acoustic wave may have approximately satisfied the Bragg condition and may have contributed to the enhanced ion line power in the time interval of 12:16:20–12:17:00 UT, whereas the PDI had not been excited until 12:17:00 UT.

Moreover, the spatiotemporal uncertainty, such as the change in the profiles of ion mass and electron density at the critical altitude, may have had a significant impact on the PDI matching condition. One can see in Figure 2 that the HFIL was delayed at 13:31, 14:01, and 14:16 UT. In Figure 1, however, the ionosphere background is in the under-dense condition for the O mode pumping and in the over-dense condition for the X mode pumping at 13:31 and 14:01 UT, whereas it is in the under-dense condition for the O/X mode pumpings at 14:16 UT. Especially, the critical frequency significantly drops or rises at 14:01 and 14:16 UT, respectively, which was probably due to changes in the profile of electron density and may have resulted in the absence of the excited condition of PDI. However, it is unexpected and confusing that the HFIL was delayed by 10 s in the over-dense and quiet condition that accompanied O/X mode pumping at 12:46 UT, whereas it was not delayed at 13:16 and 13:46 UT, when the ionosphere background was in the over-dense condition for the X mode pumping and in under-dense condition for the O mode pumping. In particular, the critical frequency dropped significantly at 13:16 UT. Thus, the PDI induced by the X mode pumping, suggested by Wang X et al. (2016a), may be an alternative explanation. As another alternative suggestion, ionosphere conditions may be an important factor in the study of delay of HFIL in the initial evolution. Indeed, the O/X mode pumpings were operating near the critical frequency, which was fluctuating in the ionosphere at the time of observations. Repeating this study under quieter ionosphere conditions would remove spatiotemporal background uncertainties, making possible a more definitive examination of the interaction between the ionosphere plasma and the O/X mode pumping.

4.   Summary and Conclusions

The experiment involving the EISCAT heater and UHF ISR was carried out at EISCAT. The ISR observations demonstrated that, in some heating cycles, the HFIL and HFPL did not appear immediately after the pumping onset, but were delayed by a few seconds.

The HFIL and HFPL delays were observed in both O/X mode pumpings, but appeared more frequently in the X mode pumping. Considering the inevitable leakage of the EISCAT heater, uncertainties in the gain pattern model, the low threshold of PDI, and the spatiotemporal uncertainty at the critical altitude, we nevertheless suggest that leakage of the X mode pumping to the O mode pumping should not be ignored.

In the initial evolution, there is a spatiotemporally positive correlation between the delay of HFIL and the delay of enhanced ${T_{\text{e}}}$, implying that the PDI may have been excited immediately after the pumping onset, but the Bragg condition may not be satisfied so that the HFIL was not observed by the ISR until ${T_{\text{e}}}$ was enhanced up to ~2500–5000 K on the traveling path. On the other hand, in the initial evolution, the spatiotemporal uncertainty at the critical altitude may result in the lack of the Bragg condition, and then the HFIL is delayed.

It cannot be ruled out that the PDI was not excited in the initial evolution. A case study shows that the natural ion line contributes to the power of HFIL in the initial evolution when ${T_{\text{e}}}$ is enhanced. Similarly, the spatiotemporal uncertainty at the critical altitude may have had a significant impact on the interaction between the O/X mode pumpings and the ionosphere, and the possibility of under-dense heating cannot be ignored. Indeed, repetition of this study in a quiet ionosphere should be pursued and the further investigation is expected.

Acknowledgments

EISCAT is an international scientific association supported by China, Finland, Japan, Norway, Sweden and the UK. Authors thank Russian colleagues for their significant efforts in performing the experiment, and Dr. Michael. T. Rietveld for the discussion of the gain pattern of the EISCAT heater. The data can be obtained at https://portal.eiscat.se/schedule/.