The nature of electron density enhancement over a wide altitude range during ionosphere heating experiments at EISCAT

1.   Introduction

In the F region of the ionosphere (altitudes >160 km), powerful high-frequency (HF) pump waves can regularly induce an appreciable change in electron density in the vicinity of the HF pump wave reflection altitude. Some studies in the past have typically observed such electron density modifications or theorized they exist. Utlaut and Violette (1972) inferred a ~7% decrease in the electron density from ionograms recorded at the Platteville Atmospheric Observatory, Colorado, USA (henceforth referred to as Platteville). Later, using the typical parameters at the Arecibo Observatory, Puerto Rico (henceforth referred to as Arecibo), and at Platteville, Meltz et al. (1974) suggested a theoretical decrease of ~3% in electron density 2 min after the onset of HF pumping. Experiments by Djuth et al. (1987) at Arecibo demonstrated that a decrease of ~10%–15% in the electron density was accompanied by a 1000–2000 K increase in the electron temperature. Duncan et al. (1988) reported the first thermally driven decrease of ~50% in electron density. However, observations at the European Incoherent Scatter Scientific Association (EISCAT) showed both an increase and a decrease in electron density in the vicinity of the reflection altitude of the HF pump wave, demonstrating disagreements with a time-dependent numerical model (Stocker et al., 1992). At the High-frequency Active Auroral Research Program (HAARP), Alaska, USA, Pedersen et al. (2010, 2011) observed a large enhancement in electron density at the altitude of ~220 km induced by the HF pump wave near the second electron gyroharmonic.

In recent years, an apparent enhancement in the electron density, induced by HF pump waves in the X mode (Senior et al., 2013) and O mode (Wu J et al., 2016, 2017), was observed over a wide range of altitudes above the pump wave reflection altitude. Senior et al. (2013) found that the shape of the enhanced ion line corresponded very closely to that of the ion line taken before the onset of pumping at the altitude of ~300 km, and that the frequency of the plasma line showed no appreciable change at the altitudes of ~321 and ~339 km. It was suggested that the apparent enhancement did not, in fact, correspond to a true enhancement in electron density. Instead, it corresponded to the enhanced ion line by some unknown mechanisms, which preferentially scatters the radar wave back along the magnetic field line. Rietveld and Senior (2020) proposed that medium- and large-scale field-aligned irregularities could refract the radar wave along the magnetic field. This could cause a strong radar backscatter, appearing in the observation as an enhanced electron density. However, Blagoveshchenskaya et al. (2022) claimed that this apparent enhancement did correspond to a true enhancement in electron density and might be due to increased ionization resulting from the flux of accelerated electrons. Indeed, the debate continues over the apparent or true nature of this enhancement in electron density, and conclusive proofs are still expected.

It is essential to confirm the apparent or true nature of the ionospheric electron density enhancement, on which the research path of physical mechanisms heavily depends. That is, if the apparent enhancement does, in fact, correspond to a true enhancement in electron density, the research of physical mechanisms will focus on the interaction between the HF pump wave and the ionospheric plasma; otherwise, it should focus on the scattering process of the radar wave. In this work, an alternative method, confirming the apparent or true nature of the ionospheric electron density enhancement, is presented, and two ionospheric heating experiments are examined.

2.   Experiment and Data

At EISCAT, near Tromsø, Norway (69.58°N, 19.21°E), the heating facility can radiate an O/X mode HF pump wave in the frequency range of 4.0–8.0 MHz (Rietveld et al., 1993). It also hosts an ultra-high-frequency (UHF) incoherent scatter radar (ISR), operating at 930.0 MHz (Rishbeth and van Eyken, 1993). In this study, we examined two prior experiments involving the aforementioned heating facility and UHF ISR:

(1) The first experiment (henceforth referred to as Experiment 1) was conducted by Senior et al. (2013) on October 18, 2012, between 13:10 and 14:50 universal time (UT). The heating facility was operated at 7.953 MHz, pointing in the field-aligned direction (12° with the zenith, 186° with the azimuth) and with an effective radiated power of ~840.0 MW. The HF pump wave was modulated to stay on for 300 s, followed by a break of 300 s, with the polarization switching between the O and X modes on successive pulses, making an overall cycle of 1200 s. The radar beam began in the field-aligned direction for the first 120 s, followed by an alignment of 11° and 13° away from the zenith for 60 s each. Finally, the radar beam was returned to the field-aligned direction for 60 s before the HF pumping was turned off. The radar power was measured at ~1.5 MW, with the HF pumping on, and at ~1.6 MW, with the HF pumping off. The system temperature of the ISR remained at ~95 K throughout Experiment 1, and some deviations from 95 K appeared occasionally, of which the apparent enhancement in the electron density is independent temporally.

(2) The second experiment (henceforth referred to as Experiment 2) was conducted by Wu J et al. (2016, 2017) on March 11, 2014, between 12:30 and 14:30 UT. The heating facility was operated at frequencies in steps of 2.8 kHz from 6.7 MHz to 7.0 MHz. The effective radiated power had a range of 56.0–78.0 MW. The O mode HF pump wave was modulated to stay on for 18 min and then, off for 12 min. The radar beam and HF pump beam stayed in the field-aligned direction throughout the experiment. The radar power was measured at ~1.4 MW, with the pumping on and at ~1.5 MW, with the HF pumping off. Throughout Experiment 2, the system temperature of the ISR was similar to that in Experiment 1 and had a value of ~100 K.

In addition, Senior et al. (2013) and Wu J et al. (2016, 2017) gave a detailed description of the two experiments, where more experimental information is available. To allow ion line smoothing, the ISR data in this study were analyzed by using an integration time of 60 s.

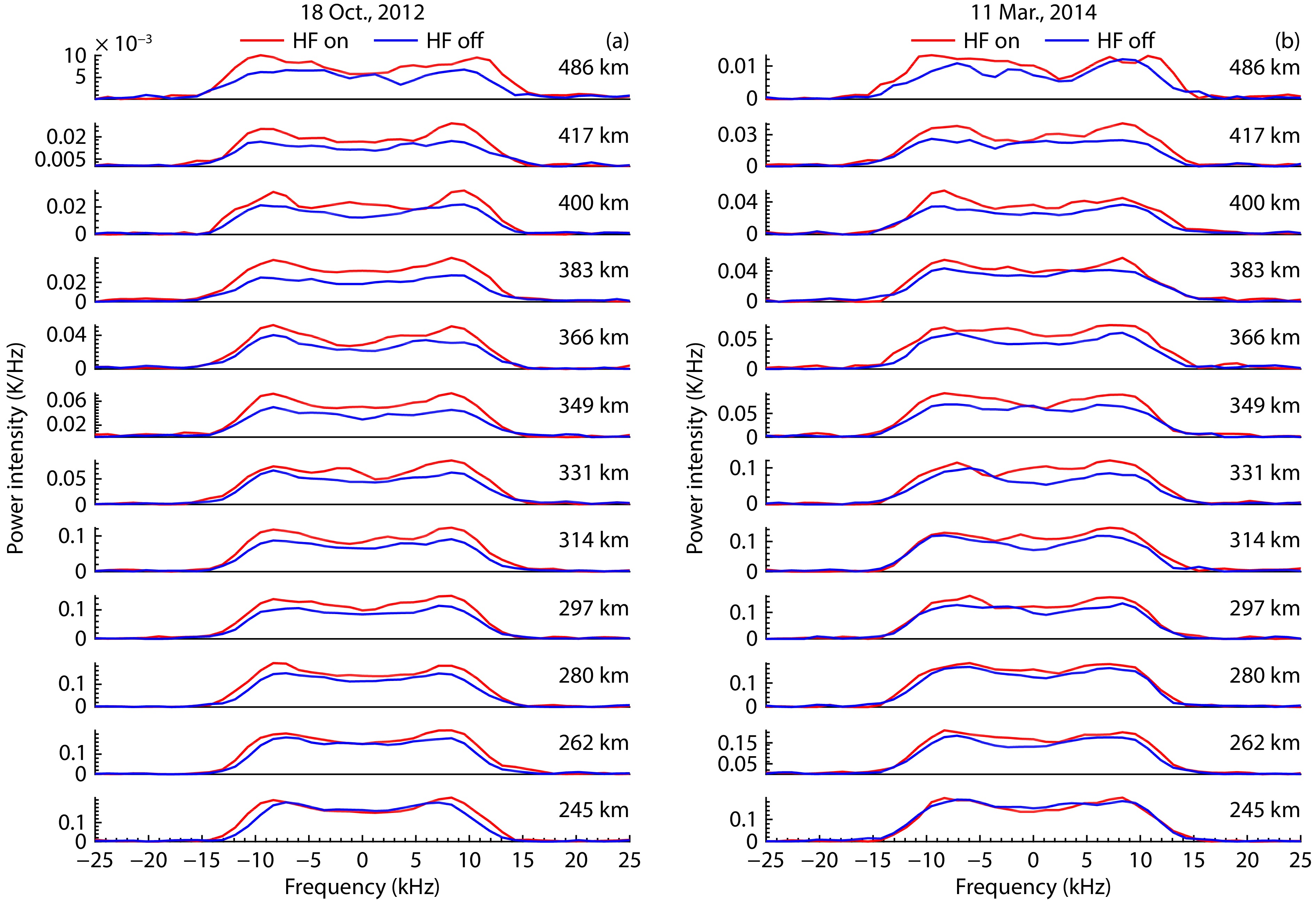
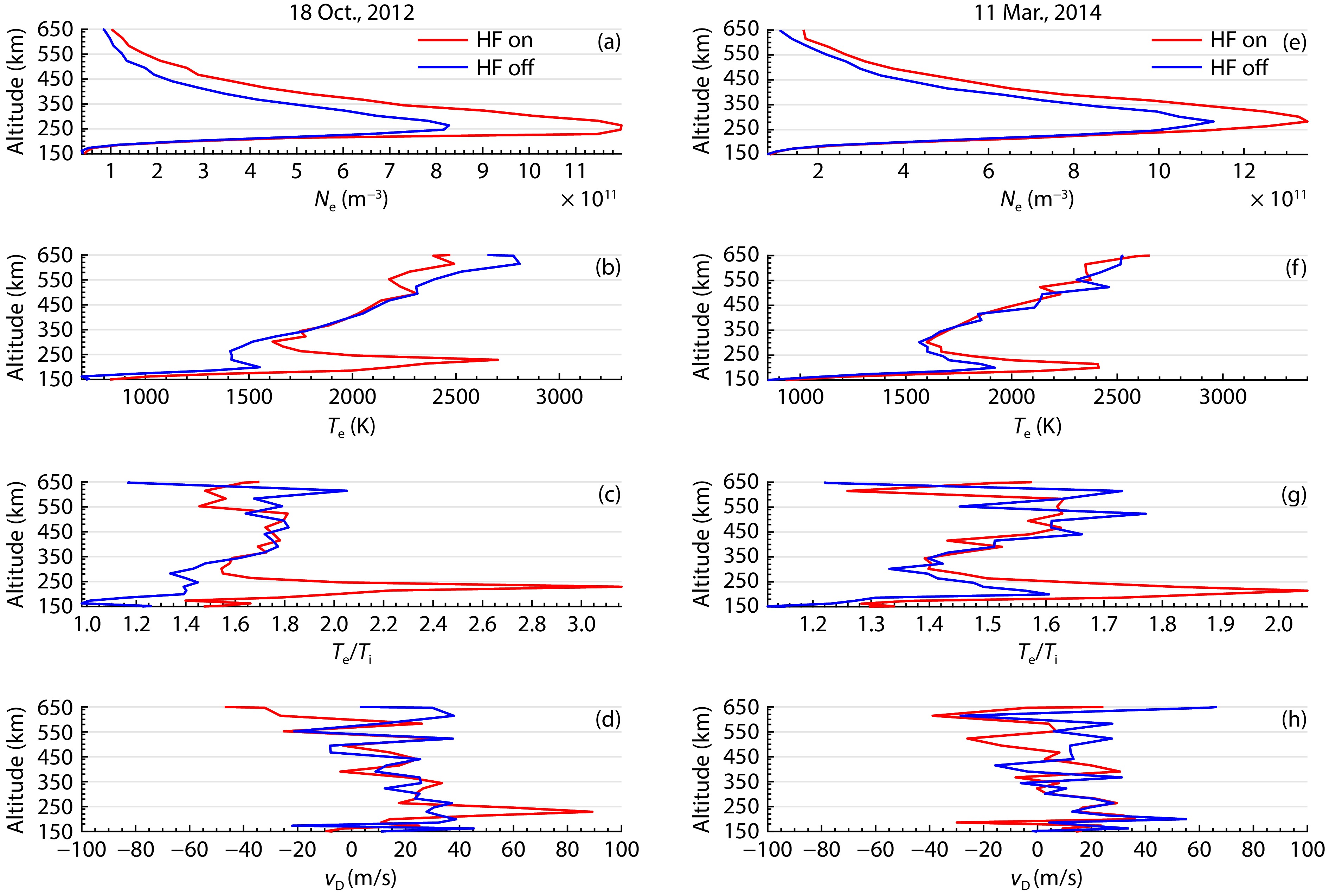
Figure 1 displays the mean electron density ${N_{\text{e}}}$, mean electron temperature ${T_{\text{e}}}$, mean ratio of electron temperature to ion temperature $\dfrac{{{T_{\text{e}}}}}{{{T_{\text{i}}}}}$, and mean ion drift velocity ${v_{\text{D}}}$. As the regular ISR observations in ionosphere heating experiments, some significant increases of ~50% and ~19% in ${N_{\text{e}}}$, ~60% and ~30% in ${T_{\text{e}}}$, and ~130% and ~30% in $\dfrac{{{T_{\text{e}}}}}{{{T_{\text{i}}}}}$ can be seen in the narrow altitude range of ~200–300 km for Experiments 1 and 2, respectively. Here, the increases in ${T_{\text{e}}}$ and $\dfrac{{{T_{\text{e}}}}}{{{T_{\text{i}}}}}$ were attributed to (i) the weak leakage of the X mode pump wave into the O mode by Senior et al. (2013), and (ii) the upper hybrid resonance close to the reflection altitude of the HF pump wave by Wu J et al. (2017). And the increase in ${N_{\text{e}}}$ was not a true enhancement in electron density but was due to the enhanced ion lines by the parametric decay instability near the reflection altitude of the HF pump wave (Robinson, 1989). In addition, because of the weaker ISR echo from a scattering volume above the altitude of ~500 km, the smaller signal-to-noise ratio (SNR) leads to contaminated profiles of ${T_{\text{e}}}$, $\dfrac{{{T_{\text{e}}}}}{{{T_{\text{i}}}}}$, and ${v_{\text{D}}}$ above an altitude of ~500 km. Moreover, because ${N_{\text{e}}}$ is dependent on only the power of the ion lines, the profile of ${N_{\text{e}}}$ is not contaminated above the altitude of ~500 km. Additionally, no evidence exists of a significant change in ${v_{\text{D}}}$ throughout both experiments, that is, ${v_{\text{D}}}$ remained at ~10 m/s above the altitude of ~350 km and at ~20 m/s below the altitude of ~350 km. This result implies that ${v_{\text{D}}}$ was not disturbed by the HF pump wave and that the drift of ionospheric plasma was not active in the geomagnetic field-aligned direction.

Figure  1.  (a) Mean electron density; (b) mean electron temperature; (c) mean ratio of electron temperature to ion temperature; and (d) mean ion drift velocity measured in Experiment 1. Each enhanced (red) or background (blue) value is the mean of the integration of the X mode pump wave, over the final 60 s of the on/off period, for five cycles. Subplots (e), (f), (g), and (h) correspond to (a), (b), (c), and (d), respectively, for Experiment 2, and the description follows that of Experiment 1 but measured over only three on/off cycles. The values were obtained by using the Grand Unified Incoherent Scatter Design and Analysis Package (GUISDAP; Lehtinen and Huuskonen, 1996).

DownLoad: Full-Size Img PowerPoint

In particular, in both cases, unexpected enhancements of ~43% and ~30% in ${N_{\text{e}}}$ were observed above the altitude of ~300 km until the altitude limit of the radar measurement. This result was consistent with a clear enhancement in the ion lines within the altitude range of 245–486 km, as illustrated in Figure 2.

Figure  2.  (a) Examples of ion lines measured in Experiment 1; (b) examples of ion lines measured in Experiment 2. The ion lines were obtained by using the EISCAT Real Time Graphic (RTG) package. The ion lines above the altitude of ~500 km are not shown because of the smaller SNR of the ISR echo. Additionally, the ion line measurement follows the same method as in Figure 1.

DownLoad: Full-Size Img PowerPoint

Figure 2 illustrates examples of ion lines in the altitude range of ~245–500 km for both experiments. It is evident that in both cases, when the pumping is on, the ion lines at ~9.5 kHz are significantly enhanced in intensity. According to the standard analysis of incoherent scatter, this observation would indicate that the profile of electron density ${N_{\text{e}}}$ is modified by the HF pumping. Moreover, the intensity of the ion lines below an altitude of ~314 km are an order of magnitude more intense than the intensity above the altitude of ~314 km, that is, depending on the ${N_{\text{e}}}$ profile and the radar echo scattered from the scattering volume.

To summarize, as observed in Figures 1 and 2, a notable enhancement is seen in ${N_{\text{e}}}$ and the ion lines in the altitude range of ~300–500 km when the HF pumping is on. It should be emphasized that the apparent enhancements are unexpected because (i) the HF pump wave should be reflected at its reflection altitude (i.e., the ionosphere above the reflection altitude should not be disturbed by the pump wave; Robinson, 1989), and (ii) only ${N_{\text{e}}}$ was enhanced, whereas other parameters remained unchanged.

3.   Discussion

Because the parameters and ion lines described in Section 2 were obtained by using the GUISDAP and RTG, which are based on the standard incoherent scatter analysis, a Maxwellian plasma is assumed here. In addition, considering the reflection of the HF pump wave near the altitude of 240 km and the unchanged profiles of ${T_{\text{e}}}$, $\dfrac{{{T_{\text{e}}}}}{{{T_{\text{i}}}}}$, and ${v_{\text{D}}}$ in the altitude range of ~300–500 km, one should be confident in the Maxwellian assumption.

For $\dfrac{{{T_{\text{e}}}}}{{{T_{\text{i}}}}} \leqslant 4$, the incoherent backscattered power ${P_{\text{r}}}$ can be expressed as (Evans, 1969; Djuth et al., 1987; Duncan et al., 1988)

where ${\sigma _{\text{e}}}$ is the Thomson cross section for electrons. In Figures 1c and 1g, $\dfrac{{{T_{\text{e}}}}}{{{T_{\text{i}}}}}$ shows no appreciable change in the altitude range of ~300–500 km in either experiment, implying that the ion lines in Figure 2 were enhanced only as a result of the enhanced ${N_{\text{e}}}$, as indicated by Equation (1). On the other hand, ${N_{\text{e}}}$ is enhanced solely because of the enhanced ion line, as indicated by the standard analysis of incoherent scatter. Thus, the enhanced ${N_{\text{e}}}$ is equivalent to the enhanced ion line (i.e., a closed relationship exists between the enhanced ${N_{\text{e}}}$ and the enhanced ion line), which satisfies the incoherent scatter theory. Obviously, for confirming the apparent or true nature of the enhanced ${N_{\text{e}}}$, examining the ion line intensity becomes invalid. Hence, instead of the ion line intensity, we will examine the ion line frequency.

For the quasi-neutral F region of the ionosphere, an ion acoustic wave should satisfy (Robinson, 1989; Kohl et al., 1993; Alcaydé, 1995)

where ${\omega _{\text{i}}}$, ${k_{\text{i}}}$, $\gamma$, ${K_{\text{B}}}$, and ${M_{\text{i}}}$ denote the angular frequency, wave number, adiabatic index, Boltzmann constant, and effective ion mass, respectively. In the case of backscatter, the ISR can observe only an ion acoustic wave satisfying the Bragg condition ${k_{\text{i}}} = 2{k_{\text{r}}}$, where ${k_{\text{r}}}$ denotes the wave number of the ISR and has a value of 19.5 m⁻¹ for the UHF ISR at EISCAT. This result implies that all the ion lines observed in Experiments 1 and 2 (Figure 2) satisfy the Bragg condition. In other words, ${k_{\text{i}}} = 39{\text{ }}{{\text{m}}^{ - 1}}$ is a constant for all the ion lines examined, although those ion acoustic waves within a small range of $2{k_{\text{r}}}$ may also contribute (Hagfors, 2003). Moreover, in both experiments, the profiles of ${T_{\text{e}}}$ and $\dfrac{{{T_{\text{e}}}}}{{{T_{\text{i}}}}}$ are independent of the HF pumping in the altitude range of ~300–500 km (Figures 1b, 1c, 1f, and 1g); that is, although some natural variability exists in the profiles of ${T_{\text{e}}}$ and $\dfrac{{{T_{\text{e}}}}}{{{T_{\text{i}}}}}$, they can still be considered to have a quasi-constant profile in the altitude range of interest. In other words, it can reasonably be considered that the profiles of ${T_{\text{e}}}$ and $\dfrac{{{T_{\text{e}}}}}{{{T_{\text{i}}}}}$ remained unchanged in the altitude range of ~300–500 km throughout both experiments. Thus, the straightforward relation between ${\omega _{\text{i}}}$ and ${M_{\text{i}}}$ is obtained as

where $\alpha = \left( {\dfrac{\gamma }{{{{{T_{\text{e}}}}/ {{T_{\text{i}}}}}}}{\text{ + }}1} \right){K_{\text{B}}}{T_{\text{e}}}k_{\text{i}}^2$ is a quasi-constant profile in the altitude range of interest.

Equation (3) indicates that, throughout the experiments, the profile of ${\omega _{\text{i}}}$ is dependent on that of ${M_{\text{i}}}$, namely, the change in ${\omega _{\text{i}}}$ should be dependent on the change in ${M_{\text{i}}}$. Figure 3 demonstrates the ratio of the enhanced ion line angular frequency $\omega _{\text{i}}^{{\text{on}}}$ to the background ion line angular frequency $\omega _{\text{i}}^{{\text{off}}}$ as a function of altitude. As shown in Figure 3, note that the SNR of this ratio in Experiment 1 is obviously larger than that in Experiment 2, and especially that the SNR around ~360–380 km in Experiment 1 and around ~300–370 km in Experiment 2 are obviously small. This may be the result of (i) the higher number of observation cycles in Experiment 1 (five cycles) compared with Experiment 2 (three cycles); (ii) the higher radar power with pumping on in Experiment 1 compared with Experiment 2 (i.e., the radar echo may have been more intense during Experiment 1); (iii) the lower system temperature of the radar in Experiment 1 (~95 K) compared with Experiment 2 (~100 K); and (iv) a data processing error by the GUISDAP.

Figure  3.  (a) Ratio of the enhanced ion line frequency to the background ion line frequency, measured in Experiment 1; (b) same ratio as in (a) for Experiment 2, where the frequency is the value corresponding to the maximum intensity of the right shoulder of the ion line.

DownLoad: Full-Size Img PowerPoint

From Figure 3a, we can observe that $\dfrac{{\omega _{\text{i}}^{{\text{on}}}}}{{\omega _{\text{i}}^{{\text{off}}}}}$ has a mean of ~1.03 in the altitude range of ~270–450 km, implying that the ion line frequency was not significantly changed by the HF pumping in Experiment 1. Thus, following Equation (3), $\dfrac{{M_{\text{i}}^{{\text{off}}}}}{{M_{\text{i}}^{{\text{on}}}}}$ has a mean of ~1.06 in the altitude range of ~270–450 km, where $M_{\text{i}}^{{\text{on}}}$ denotes the effective ion mass with the pumping on and $M_{\text{i}}^{{\text{off}}}$ denotes the effective ion mass with the pumping off. Considering the aforementioned error of the SNR, this may imply that ${M_{\text{i}}}$ was not significantly changed by the HF pumping in the altitude range of ~270–450 km. However, below the altitude of ~270 km, $\dfrac{{\omega _{\text{i}}^{{\text{on}}}}}{{\omega _{\text{i}}^{{\text{off}}}}}$ has a mean of ~1.2. This change can be attributed to the natural ion acoustic waves close to $\omega _{\text{i}}^{{\text{on}}}$. Here, to distinguish them from the HF enhanced ion acoustic waves by the parametric decay instability, the natural ion acoustic waves denote the waves unaffected by the HF pump wave. The natural ion acoustic wave covers a wide frequency spectrum owing to the highly varied ion mass distribution in the ionosphere, in which some of the higher frequencies could satisfy the Bragg condition owing to the enhanced ${T_{\text{e}}}$ as indicated by Equation (2) . In other words, following Equation (2) and considering a constant ${M_{\text{i}}}$, when ${T_{\text{e}}}$ becomes higher, the ion acoustic waves at the higher frequencies will be observed. Thus, below the altitude of ~270 km, the enhanced ${T_{\text{e}}}$ leads to $\dfrac{{\omega _{\text{i}}^{{\text{on}}}}}{{\omega _{\text{i}}^{{\text{off}}}}} > 1$, for instance, at the altitude of ~230 km, the enhanced ${T_{\text{e}}}$ of ~2700 K (the ratio of the enhanced electron temperature to the background temperature $\dfrac{{T_{\text{e}}^{{\text{on}}}}}{{T_{\text{e}}^{{\text{off}}}}} \approx 2$) in Figure 1b leads to $\dfrac{{\omega _{\text{i}}^{{\text{on}}}}}{{\omega _{\text{i}}^{{\text{off}}}}} \approx 1.50$ in Figure 3a . The measurement error, resulting from the small SNR, may lead to the increased frequency ratio mean value of ~1.24 above the altitude of ~450 km. Indeed, Equation (1) indicates that ${P_{\text{r}}}$ must be reduced above the altitude of ~450 km because of the decreasing ${N_{\text{e}}}$ and increasing $\dfrac{{{T_{\text{e}}}}}{{{T_{\text{i}}}}}$, as shown in Figure 1. Similarly, the aforementioned behavior holds true for Experiment 2, namely, $\dfrac{{\omega _{\text{i}}^{{\text{on}}}}}{{\omega _{\text{i}}^{{\text{off}}}}}$ has a mean of ~1.04 in the altitude range of ~270–450 km, ~1.05 below the altitude of ~270 km, and ~1.4 above the altitude of ~450 km, as shown in Figure 3b. It is important to note that in the altitude range of ~270–450 km, although the intensity of the ion lines is enhanced when the HF pumping is on, their frequency remains unchanged. Following Equation (3), this result implies that the ${M_{\text{i}}}$ profile may remain unchanged in the altitude range of ~270–450 km.

Now, ${M_{\text{i}}}$ can be expressed as

where ${N_{\text{i}}}$ and ${m_{\text{i}}}$ denote the density and mass of ion species, respectively. The quantity ${N_{\text{i}}}{m_{\text{i}}}$ is dependent on the incident radiation and the atmospheric composition, regardless of the corpuscular ionization, which may be significant in the nighttime ionosphere (Rishbeth and Garriott, 1969). With a constant profile of atmospheric composition, a strong incident radiation could lead to an increase in ${N_{\text{i}}}$. As indices of solar activity (Nicolet and Bossy, 1985), solar radio fluxes (SRFs) were measured at 245.0, 410.0, 610.0, 1415.0, 2695.0, 4995.0, 8800.0, and 15,400.0 MHz, as shown in Figure 4. With the exception at 610.0 MHz, the SRFs do not demonstrate a significant and systematic variation in intensity during either experiment. At 610.0 MHz, the intensity of the SRF varied between ~10,000 solar flux units (SFU) in Experiment 1 and ~140,000 SFU in Experiment 2. Obviously, the SRFs do not temporally synchronize with the enhanced ${N_{\text{e}}}$. In addition, the HF pump wave was reflected at the altitude of ~240 km for Experiment 1 and at ~230 km for Experiment 2. Thus, in both experiments, it is reasonable to assume that the incident radiation does not have a significant impact on ${N_{\text{i}}}$.

Figure  4.  Solar radio fluxes above the baseline as recorded at the Radio Solar Telescope Network radio observatory in San Vito, Italy. The abscissa origin denotes 13:00 UT on October 18, 2012 (Experiment 1) and 12:20 UT on March 11, 2014 (Experiment 2).

DownLoad: Full-Size Img PowerPoint

Moreover, an analysis of the vertical drift of plasma in both experiments shows that ${v_{\text{D}}} \approx 0$, indicating no active drift of plasma along the magnetic field lines and suggesting no induced change in the ion species. Nevertheless, a further examination of the change in ion species is needed. The ionosphere is mainly composed of hydrogen ions ${{\text{H}}^ + }$, helium ions He⁺, nitrogen ions ${{\text{N}}^{\text{ + }}}$, atomic oxygen ions ${{\text{O}}^ + }$, molecular oxygen ions ${\text{O}}_2^ +$, and nitric oxide ions ${\text{N}}{{\text{O}}^ + }$ in the altitude range of interest (Robinson, 1989). The frequency of the ion acoustic wave corresponding to ${{\text{H}}^ + }$ is $\dfrac{{k}_{\mathrm{r}}}{2\pi }\sqrt{\gamma \dfrac{{K}_{\mathrm{B}}{T}_{\mathrm{e}}}{{m}_{\mathrm{i}{\mathrm{H}}^{+}}}}\approx 43.7\;\text{kHz}$, where ${k}_{\mathrm{r}}=39\;{\text{m}}^{-1}$ for the UHF radar, $\gamma$ denotes the adiabatic index, ${K_{\text{B}}}$ denotes the Boltzmann constant, ${m}_{\mathrm{i}{\mathrm{H}}^{+}}$ denotes the mass of ${{\text{H}}^ + }$, and ${T}_{\mathrm{e}}$ is ~2000 K, as given in Figure 1. This result indicates that the frequency of the ion acoustic wave corresponding to ${{\text{H}}^ + }$ does not lie in the ion line channel of [−40 kHz, 40 kHz] of the UHF ISR at EISCAT, implying that the ion acoustic wave corresponding to ${{\text{H}}^ + }$ cannot be collected by the UHF ISR. Similarly, the frequency of the ion acoustic wave corresponding to He⁺ is ~22 kHz, which deviates significantly from the ~9.5 kHz shown in Figure 2. The frequencies of the ion acoustic waves corresponding to ${{\text{N}}^{\text{ + }}}$, ${{\text{O}}^ + }$, ${\text{O}}_2^ +$, and ${\text{N}}{{\text{O}}^ + }$, respectively, are ~11.5 kHz, ~10.5 kHz, ~7.8 kHz, and ~8 kHz, all of which may contribute to the ion lines at ~9.5 kHz shown in Figure 2. Considering that the frequencies of ion lines show no significant change in Figure 2, the ion species of ${{\text{N}}^{\text{ + }}}$, ${{\text{O}}^ + }$, ${\text{O}}_2^ +$, and ${\text{N}}{{\text{O}}^ + }$ may not have been modified in the altitude range of interest. Both these analyses strongly imply that no modification has occurred in the ion species.

As a result, a straightforward relation between ${M_{\text{i}}}$ and ${N_{\text{e}}}$ can be obtained as

where $\beta {\text{ = }}\sum\limits_{\text{i}} {{N_{\text{i}}}{m_{\text{i}}}}$ is a quasi-constant profile. Equation (5) indicates that, during the course of both experiments, because no modifications occurred in ${M_{\text{i}}}$, ${N_{\text{e}}}$ must also not have been enhanced by the HF pumping in the altitude range of ~270–450 km.

4.   Summary

With regard to the apparent enhancement in electron density over a wide altitude range during the ionospheric heating experiments, the observations at EISCAT were investigated by following the dispersion relation of ion acoustic waves.

Our investigation showed no significant modifications in the ion line frequency and the electron temperature in the altitude range of interest, which strongly implies that the profile of the effective ion mass must remain unchanged. Moreover, the incident radiation and the ion drift velocity indicate that the ion species and their densities must not have been modified. With the assumption of quasi-neutrality, it can be reasonably concluded that the apparent electron density enhancement does not, in fact, correspond to a true enhancement in electron density, which preferentially supports the suggestion by Senior et al. (2013) and the proposal for a physical mechanism by Rietveld and Senior (2020).

Open Research

Data Availability Statement: The ISR and SRF data, respectively, are available free of charge for public download at https://portal.eiscat.se/schedule/ and https://www.ngdc.noaa.gov/stp/space-weather/solar-data/solar-features/solar-radio/rstn-1-second/.