Ion and electron motions in the outer electron diffusion region of collisionless magnetic reconnection

1.   Introduction

Magnetic reconnection provides a physical mechanism for conversion from magnetic energy to plasma kinetic energy and thermal energy through topologic changes of the magnetic field lines (Parker, 1957; Sweet, 1958; Priest and Forbes, 2000; Yamada et al., 2010; Hesse and Cassak, 2020). It is widely accepted that various explosive phenomena, such as solar flares, coronal mass ejections, and magnetospheric substorms, are caused by magnetic reconnection (Masuda et al., 1994; Lin J and Forbes, 2000; Angelopoulos et al., 2008; Lu QM et al., 2022). The collisionless reconnection model, which provides a fast reconnection rate, is necessary to account for these phenomena. In collisionless magnetic reconnection, the collision frequency between charged particles is negligible; therefore, the motions between ions and electrons are decoupled (Birn and Hesse, 2001; Pritchett, 2001; Shay et al., 2007; Wang RS et al., 2010; Divin et al., 2012; Lu QM et al., 2013).

Collisionless magnetic reconnection has a multiscale structure (Birn and Hesse, 2001; Pritchett, 2001; Shay et al., 2001; Lu QM et al., 2010, 2013; Zong QG and Zhang H, 2018). The scale size below the electron inertial length ${d}_{\mathrm{e}}=c$/${\omega }_{\mathrm{p}\mathrm{e}}$ (where ${\omega }_{\mathrm{p}\mathrm{e}}$ is the electron plasma frequency) around the X line forms the electron diffusion region (EDR), where both the electron and ion motions are demagnetized. In the EDR, electrons are accelerated in the out-of-plane direction by the reconnection electric field, and then leave away from the X line along the outflow direction under the action of the Lorentz force (Drake et al., 2005; Fu XR et al., 2006; Huang C et al., 2010; Cassak et al., 2017; Liu YH et al., 2017; Liu DK et al., 2021). It is implied that the electron outflow speed can reach nearly one electron Alfvén speed (Hesse et al., 2009; Cassak et al., 2017). At the scale size between the electron inertial length and ion inertial length ${d}_{\mathrm{i}}=c/{\omega }_{\mathrm{p}\mathrm{i}}$ (where ${\omega }_{\mathrm{p}\mathrm{i}}$ is the ion plasma frequency) around the X line, the electrons become frozen in the magnetic field while the ions are still essentially demagnetized. This region is called the ion diffusion region (IDR; Shay et al., 2001; Wang RS et al., 2010). The decoupling motions between ions and electrons in the IDR result in the quadrupolar structure of the Hall magnetic field (the magnetic field in the out-of-plane direction; Birn and Hesse, 2001; Nagai et al., 2003; Divin et al., 2012). At the scale size beyond the ion inertial length, the ion and electron motions are coupled together and frozen in the magnetic field, and the ion outflow speed is approximately one Alfvén speed.

Recently, both particle-in-cell (PIC) simulations and satellite observations have found that the EDR has a multiscale structure: an inner EDR around the X line and an outer EDR with a length of several ion inertial lengths (Daughton et al., 2006; Phan et al., 2007; Shay et al., 2007; Divin et al., 2016). Karimabadi et al. (2007) indicated that the electron outflow velocity increases in the inner EDR and reaches a peak value near one electron Alfvén speed, whereas the outflow jet slows down gradually in the outer EDR. However, how the electron and ion outflows change in the inner and outer EDRs until they are coupled together in the far downstream is still unclear. In this article, a two-dimensional (2D) PIC simulation model is used to study the evolution of electron and ion outflows in the inner and outer EDRs by analyzing the contributions from the Lorentz force, the electric field force, and the pressure tensor term.

2.   Simulation Model

We use a 2D PIC simulation code, which has been successfully applied to study magnetic reconnection (Fu XR et al., 2006; Huang C et al., 2010; Lu QM et al., 2010; Chang C et al., 2021). In this model, particle motions are controlled by the electromagnetic field, and the electromagnetic field is updated by solving the Maxwell equations with an explicit leapfrog algorithm.

The initial equilibrium configuration is a Harris current sheet in the (x, z) plane (Harris, 1962), where the initial magnetic field and the corresponding number density are given by

where ${B}_{0}$ is the asymptotic magnetic field, ${\text{δ}}$ is the half-width of the current sheet, ${\boldsymbol{e}}_{x}$ is the unit vector in the x direction, ${n}_{0}$ is the peak density of the current sheet, and the background density is ${n}_{b}=0.1{n}_{0}$. Ions and electrons are assumed to satisfy the Maxwellian distribution with the initial temperature ratio ${T}_{\mathrm{i}0}/{T}_{\mathrm{e}0}=4$, where ${T}_{\mathrm{e}0}$ ( ${T}_{\mathrm{i}0}$ ) is the initial temperature of electrons (ions). In our simulations, we set ${\text{δ}} =0.5{d}_{\mathrm{i}}$ (where ${d}_{\mathrm{i}}=c/{\omega }_{\mathrm{p}\mathrm{i}}$ denotes the ion inertial length defined by ${n}_{0}$), ${m}_{\mathrm{i}}/{m}_{\mathrm{e}}= 100$ (where ${m}_{\mathrm{i}}$ denotes the ion mass and ${m}_{\mathrm{e}}$ denotes the electron mass), and $c=15{V}_{A}$ (where $c$ denotes the light speed and ${V}_{A}={B}_{0}/\sqrt{{\mu }_{0}{m}_{\mathrm{i}}{n}_{0}}$ is the Alfvén speed). The simulation domain is ${L}_{x}\times {L}_{z}=80{d}_{\mathrm{i}}\times 20{d}_{\mathrm{i}}$, with the spatial resolution $\Delta x=\Delta z=0.05{d}_{\mathrm{i}}$. The time step is $\Delta t=0.001{\Omega }_{\mathrm{i}}^{-1}$ (where ${\Omega }_{\mathrm{i}}=e{B}_{0}/{m}_{\mathrm{i}}$ is the ion gyrofrequency). A periodic boundary condition is assumed in the x direction, whereas in the z direction, we use a conducting boundary condition. We give an initial magnetic flux perturbation to trigger magnetic reconnection quickly.

3.   Simulation Results

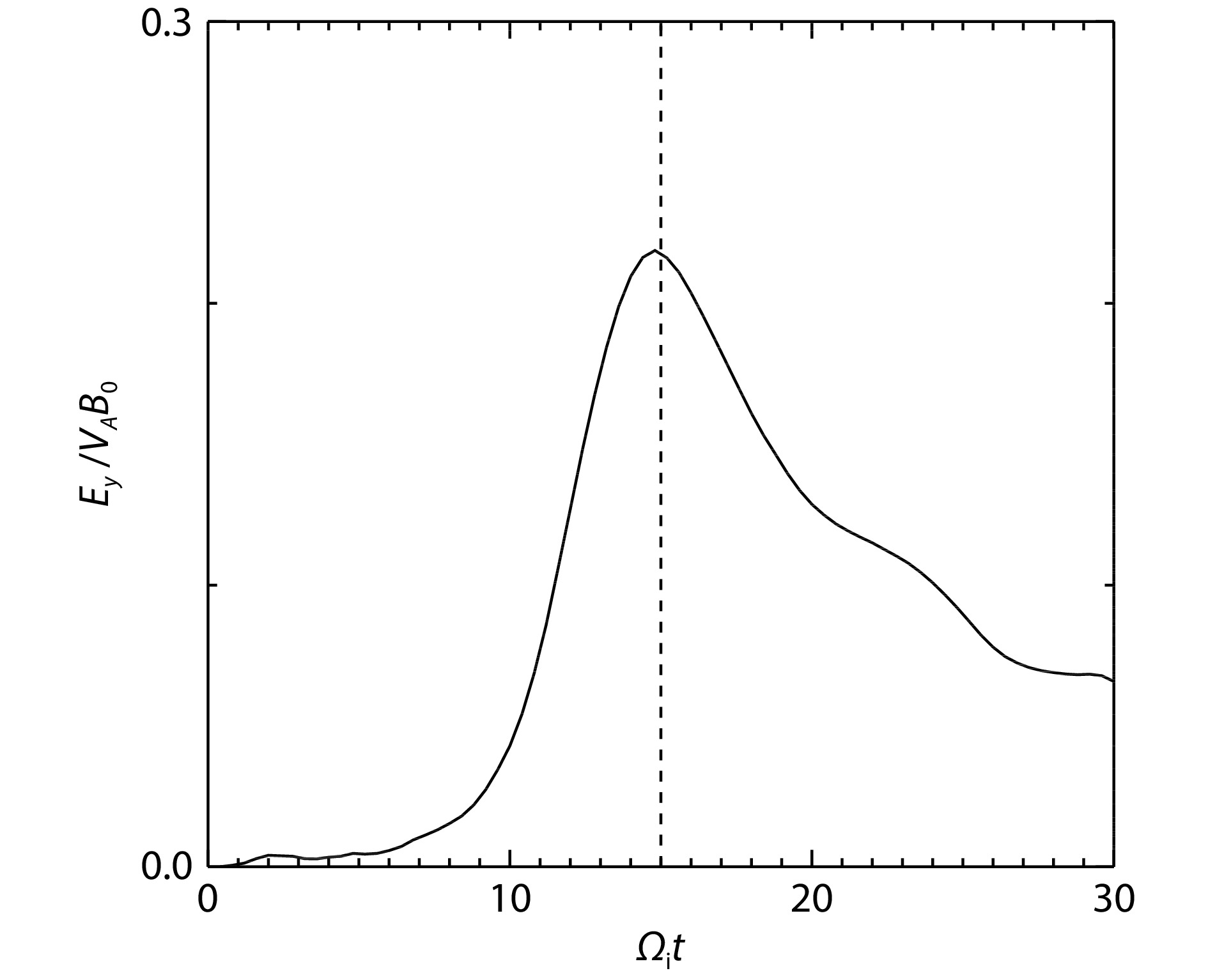
Figure 1 shows the time evolution of the reconnection rate, which is defined as the reconnection electric field ${E}_{y}$ at the reconnection site, normalized by ${{V}_{A}B}_{0}$. Previous research studies have shown that the process of reconnection has two stages. At the first stage, the tearing mode is excited, and it saturates quickly. Therefore, the tearing mode can provide only the initial growth of the reconnection. The second stage begins with the formation of the reconnection X line, which is a fast reconnection process (Lu QM et al., 2013). From the figure, we can see that magnetic reconnection occurs around ${\Omega }_{\mathrm{i}}t=8$, when the reconnection electric field begins to increase rapidly. Before that time, the current sheet is unstable to the tearing mode, and only one major X line is fully developed at approximately x = 40${d}_{\mathrm{i}}$. Magnetic reconnection saturates at approximately ${\Omega }_{\mathrm{i}}t=15$, and at that time the reconnection electric field reaches the maximum, approximately ${E}_{y}=0.22{{V}_{A}B}_{0}$. It then slowly decreases, and reconnection evolves into a quasi-steady stage.

Figure  1.  Temporal evolution of the reconnection electric field ${E}_{y}$ at the reconnection site. The reconnection rate reaches the maximum at approximately ${\Omega }_{\mathrm{i}}t=15$, which is represented by the dashed line.

DownLoad: Full-Size Img PowerPoint

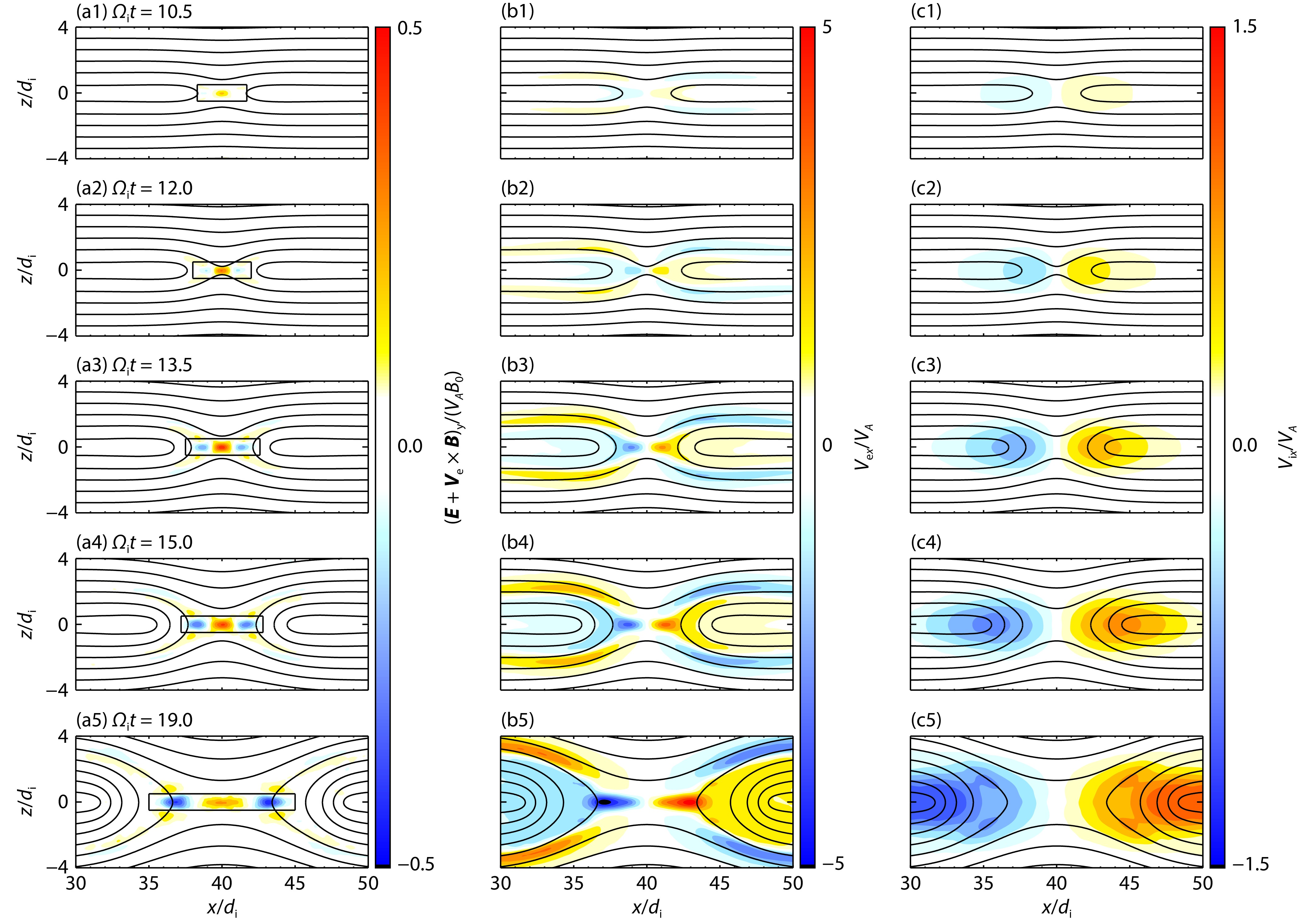
Figure 2 shows the evolution of a non-ideal electric field ${\left(\boldsymbol{E}+{\boldsymbol{V}}_{\mathrm{e}}\times \boldsymbol{B}\right)}_{y}$, the electron and ion outflows in the x direction at ${\Omega }_{\mathrm{i}}t$ = 10.5, 12, 13.5, 15, and 19. The figure clearly shows that the EDR has a two-scale structure of inner and outer layers. The inner EDR is defined as the region where the non-ideal electric field is positive ${\left(\boldsymbol{E}+{\boldsymbol{V}}_{\mathrm{e}}\times \boldsymbol{B}\right)}_{y} > 0$, near the reconnection site. In the outer EDR, the non-ideal electric field is negative ${\left(\boldsymbol{E}+{\boldsymbol{V}}_{\mathrm{e}}\times \boldsymbol{B}\right)}_{y} < 0$, and its length can extend to several ion inertial lengths. Within the two-scale EDR is a strong electron outflow jet, which is much faster than the Alfvén speed, and the peak speed of the jet can reach approximately 5${V}_{A}$. After leaving the EDR, the electrons are remagnetized and leave away from the X line along the separatrices. The ions can also be accelerated in the outer EDR, and the peak value of the outflow can reach approximately 1${V}_{A}$.

Figure  2.  The evolution of (a1–a5) the non-ideal electric field ${\left(\boldsymbol{E}+{\boldsymbol{V}}_{\mathrm{e}}\times \boldsymbol{B}\right)}_{y}$, (b1–b5) electron outflow in the x direction ${V}_{\mathrm{e}x}$, and (c1–c5) ion outflow in the x direction ${V}_{\mathrm{i}x}$ at ${\Omega }_{\mathrm{i}}t$ = 10.5, 12, 13.5, 15, and 19, respectively. The scale of the EDR is defined by the region where the non-ideal electric field is nonzero, as represented by the black boxes in panels a1–a5.

DownLoad: Full-Size Img PowerPoint

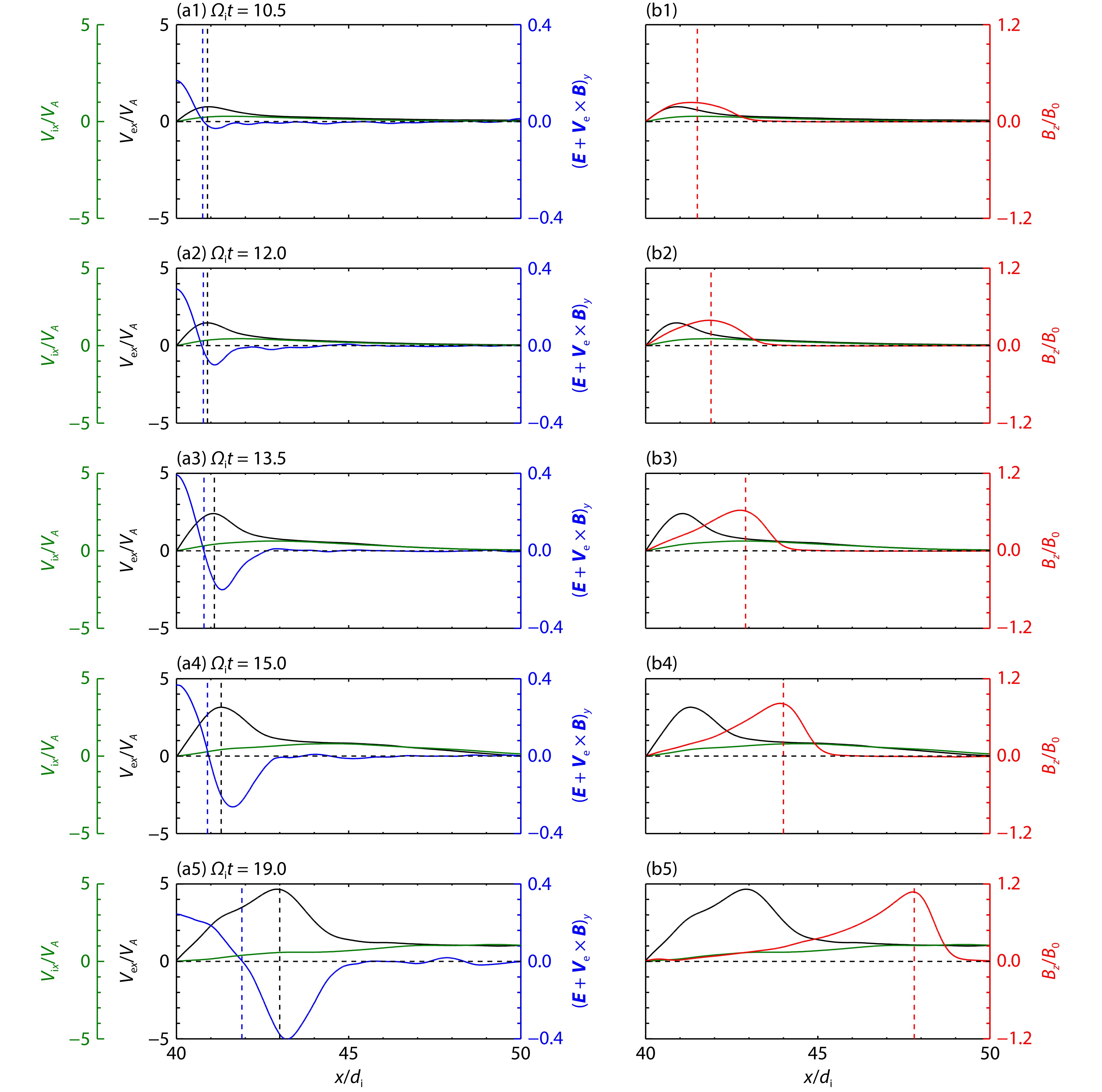
To show the electron and ion outflows in the EDR more clearly, Figures 3a1–3a5 describe the profiles of the electron outflow velocity ${V}_{\mathrm{e}x}$, the ion outflow velocity ${V}_{\mathrm{i}x}$, and the non-ideal electric field ${\left(\boldsymbol{E}+{\boldsymbol{V}}_{\mathrm{e}}\times \boldsymbol{B}\right)}_{y}$ along the line z = 0. The boundary of the inner EDR is identified based on the condition ${\left(\boldsymbol{E}+{\boldsymbol{V}}_{\mathrm{e}}\times \boldsymbol{B}\right)}_{y}=0$, as indicated by the blue dashed line. The electrons are accelerated around the X line to form an outflow jet, and the electron bulk flow first increases and then decreases in the outer EDR. The ions continuously accelerate and then recouple together with the electrons downstream of the outer EDR. Figures 3b1–3b5 describe the profiles of the magnetic field ${B}_{z}$ along the line z = 0, as indicated by the red lines. The pileup of the magnetic field occurs in the outflow region, and the peak of ${B}_{z}$ is located downstream of the electron brake region.

Figure  3.  (a1–a5) The cuts of the electron outflow velocity ${V}_{\mathrm{e}x}$ (black line), the ion outflow velocity ${V}_{\mathrm{i}x}$ (green line), and the non-ideal electric field ${\left(\boldsymbol{E}+{\boldsymbol{V}}_{\mathrm{e}}\times \boldsymbol{B}\right)}_{y}$ (blue line) along the line z = 0, respectively. Here, the black dashed lines mark the location where ${V}_{\mathrm{e}x}$ peaks, and the blue dashed lines mark the boundary of the inner EDR. (b1–b5) The cuts of the magnetic field in the z direction ${B}_{z}$ (red line), the electron outflow velocity ${V}_{\mathrm{e}x}$ (black line), and the ion outflow velocity ${V}_{\mathrm{i}x}$ (green line) along the line z = 0, respectively. Here, the red dashed lines mark the location where ${B}_{z}$ peaks.

DownLoad: Full-Size Img PowerPoint

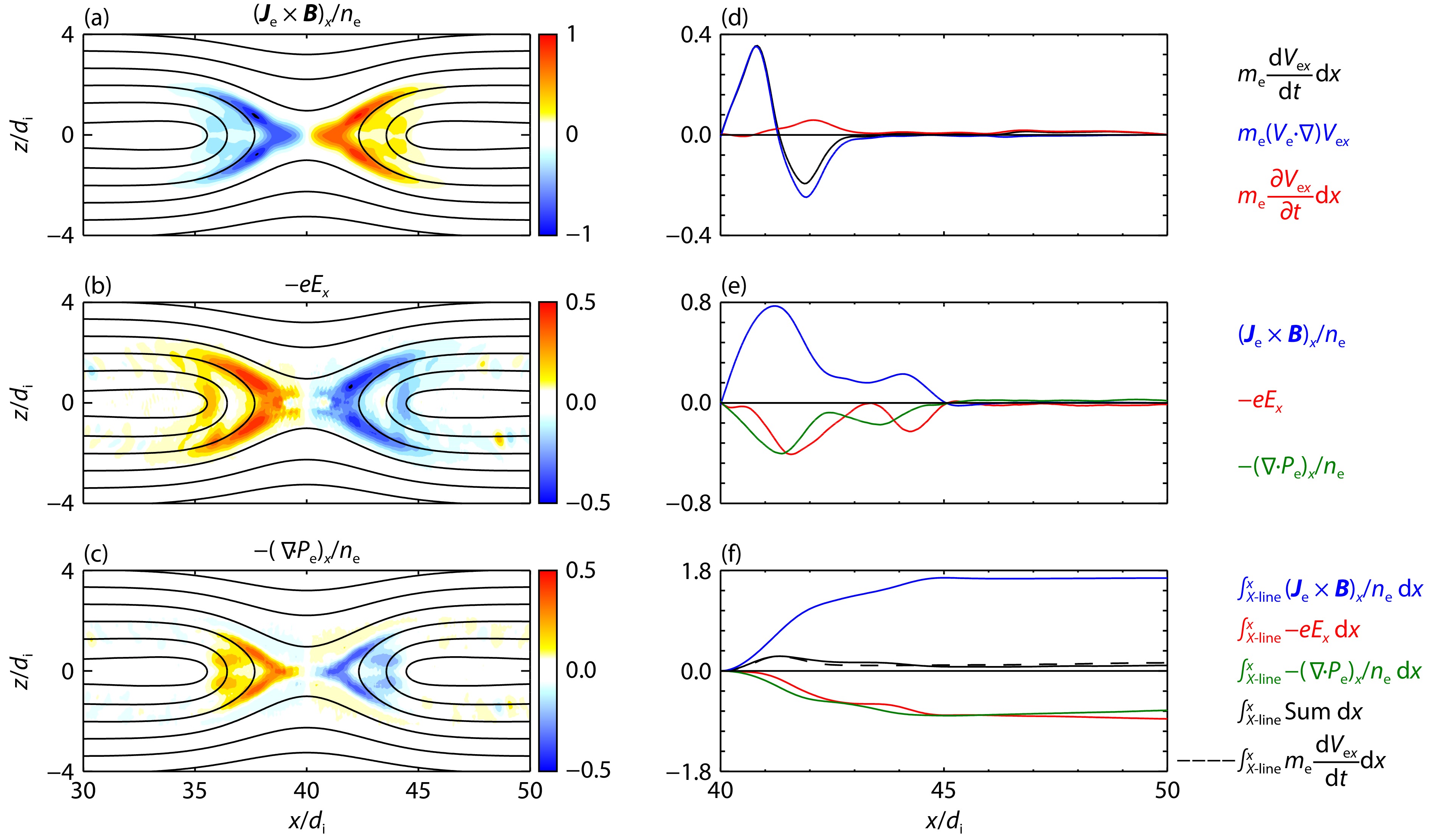
To describe the electron outflow in detail, the distribution of forces on electrons that are considered fluids can be analyzed. The electron jet near the X line is almost along the x direction, and we consider only the x component of the electron momentum equation,

The terms on the right are the electric field force, Lorentz force, and electron pressure gradient force, respectively.

Figure 4 shows the x component of (a) the Lorentz force term, (b) the electric field force term, and (c) the electron pressure gradient force term at ${\Omega }_{\mathrm{i}}t=15$. On the right side of the X line, the Lorenz force is positive, whereas the electric field force and the electron gradient force are opposite. The Lorenz force tends to convert the direction of the accelerated electron velocity to the x direction, forming the electron outflow. Although the contribution of the Lorentz force dominates, both the electric field force and the electron gradient force attempt to drag the electron outflow. The Hall electric field ${E}_{x}$ is predominantly electrostatic and is caused by charge separation, owing to different electron and ion motions in the magnetic fields (Lu S et al., 2021). The electron temperature generally increases in the EDR and the outflow region (Wang S et al., 2016), and the resulting pressure gradient leads to the deceleration of the electron outflow. These results can easily be seen in Figure 4e, giving the profile of the three force terms on the electron along the line z = 0. The left side of Equation (3) can be expressed as

Figure  4.  The x component of the force terms on the right side of the electron momentum equation, (a) the Lorentz force term, (b) the electric field force term, and (c) the electron pressure gradient force term at ${\Omega }_{\mathrm{i}}t=15$. The profile of (d) on the left side of the electron momentum equation, (e) the three force terms on the electron, and (f) the integral of the electron momentum equation along z = 0. The red lines are the electric field term, the blue lines are the Lorentz force term, and the green lines are the electron pressure gradient force term in panels (e) and (f). The black dashed lines are the left side of the electron momentum equation (Equation (3)), and the black lines are the sum of the three force terms in panel (e).

DownLoad: Full-Size Img PowerPoint

The $\left({\boldsymbol{V}}_{\mathrm{e}}\cdot \nabla \right){V}_{\mathrm{e}x}$ term is much larger than the $\dfrac{\partial {V}_{\mathrm{e}x}}{\partial t}$ term, which means that the spatial variation of electron outflow ${V}_{\mathrm{e}x}$ dominates (Figure 4d). After integrating Equation (3) in the x direction along z = 0, we get

where the integration is calculated from the position X line to x. Figure 4f plots the profiles of the integrated terms in Equation (4), and we find that the two sides of the equation are almost balanced.

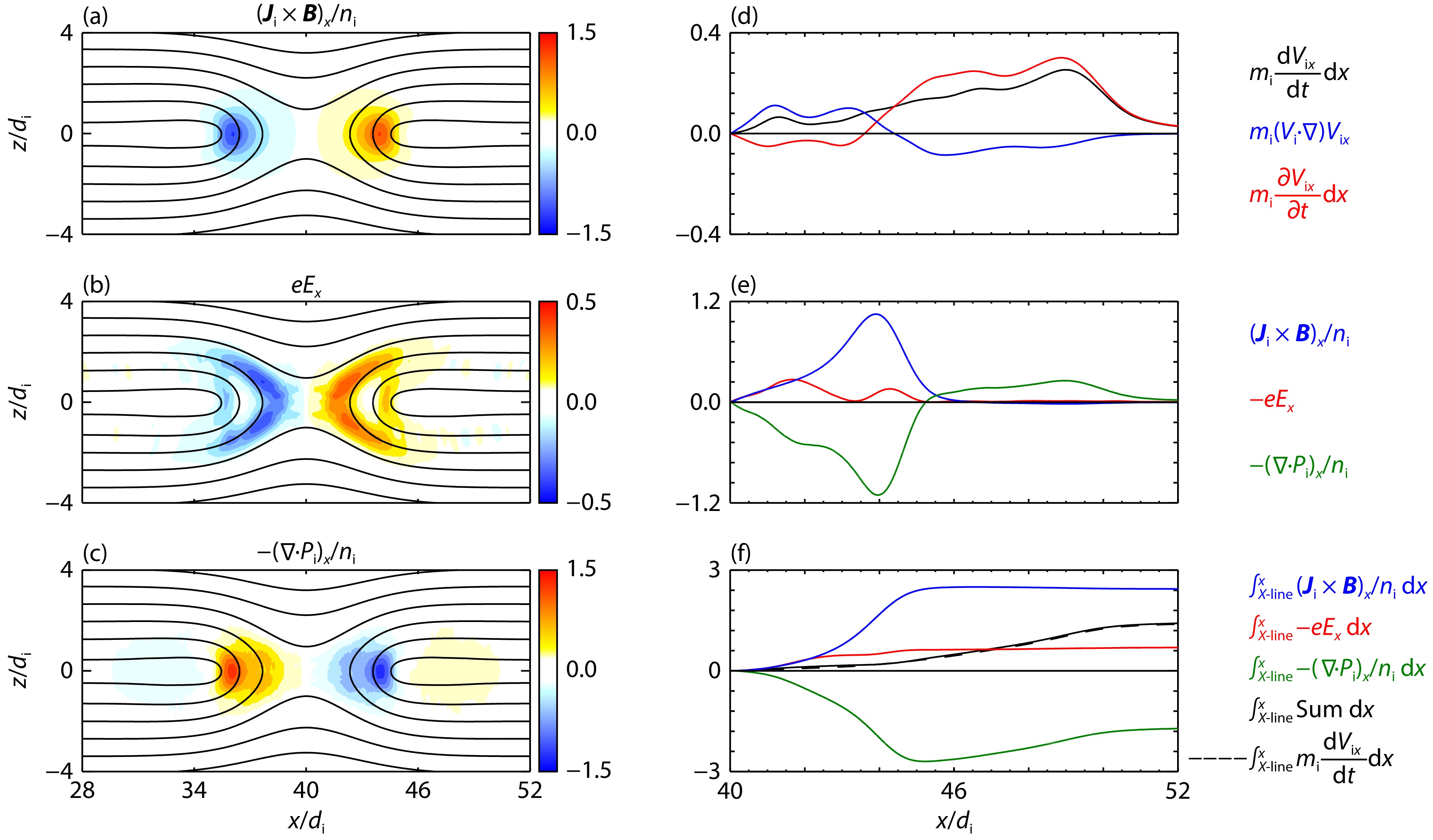
A similar force analysis is done on ions, and the x component of the ion momentum equation can be written as

Figures 5a–5c show the three terms on the right side of Equation (5). On the right side of the X line, both the Lorentz force and the electric field force are positive such that the ion velocity increases to form an ion outflow, but the ion pressure gradient force is opposite (as shown in Figure 5e). Figure 5f plots the profiles of the integrated terms in Equation (5), and we can see that the black dashed curve and the black solid curve almost overlap, indicating that Equation (5) is satisfied well in our simulation. The sum of the three forces on the right side of Equation (5) is always positive, indicating that the ions are continuously accelerated. Although the Lorentz force and the ion pressure gradient force are much larger than the Hall electric field force, their effects on the ions are almost balanced. Therefore, the Hall electric field force, which does positive work on ions, is a small value but cannot be ignored. The spatial distribution of the outflow velocity corresponds to the $\left({\boldsymbol{V}}_{\mathrm{i}}\cdot \nabla \right){V}_{\mathrm{i}x}$ term, which has a positive and negative inversion in the x direction. The negative value of $\left({\boldsymbol{V}}_{\mathrm{i}}\cdot \nabla \right){V}_{\mathrm{i}x}$ is offset by the positive value of $\dfrac{\partial {V}_{\mathrm{i}x}}{\partial t}$; therefore, the $\dfrac{\mathrm{d}{V}_{\mathrm{i}x}}{\mathrm{d}t}$ is always positive (Figure 5d).

Figure  5.  The x component of the force terms on the right side of the ion momentum equation, (a) the Lorentz force term, (b) the electric field force term, and (c) the ion pressure gradient force term at ${\Omega }_{\mathrm{i}}t=15$. The profile of (d) the left side of the ion momentum equation, (e) the three force terms on the ion, and (f) the integral of the ion momentum equation along z = 0. The red lines are the electric field term, the blue lines are the Lorentz force term, and the green lines are the ion pressure gradient force term in panels (e) and (f). The black dashed lines are the left side of the ion momentum equation (Equation (5)), and the black lines are the sum of the three force terms in panel (f).

DownLoad: Full-Size Img PowerPoint

4.   Conclusions and Discussion

In this article, by performing a 2D PIC simulation, we identify the two-scale structure of the EDR in collisionless magnetic reconnection. The inner EDR is defined as the region where ${\left(\boldsymbol{E}+{\boldsymbol{V}}_{\mathrm{e}}\times \boldsymbol{B}\right)}_{y} > 0$, whereas ${\left(\boldsymbol{E}+{\boldsymbol{V}}_{\mathrm{e}}\times \boldsymbol{B}\right)}_{y} < 0$ in the outer EDR. In the inner EDR, the bidirectional electron jet emits from the X line, and the speed of the electron outflow increases. The electron jet then decelerates in the outer EDR. The lengths of the EDR and the fast electron jet are constantly elongated. To describe the electron outflow in detail, the forces on electrons that are considered fluids can be analyzed. Around the X line, the electrons are accelerated by the reconnection electric field in the out-of-plane direction. When the electrons move away from the X line, the Lorentz force converts the direction of the accelerated electrons to the x direction, yet both the electric field force and the electron gradient force tend to slow the electron outflow. For ions, the Lorentz force is positive, which tends to accelerate the ions to form an ion outflow. The pressure gradient force tends to decelerate the ion outflow. The Lorentz force is almost balanced by the pressure gradient force. The Hall electric field force does positive work on ions and is not negligible.

After analyzing the x-component of the momentum equation, Liu DK et al. (2021) suggested that the ion outflow is dominated by the Lorentz force, whereas the pressure gradient force drags the ion outflow. The effect of the electric field force on the ion outflow is absent because the electric field force term is canceled out when the electron momentum equation and the ion momentum equation are added. Karimabadi et al. (2007) indicated that the ion acceleration within the inner EDR is due to the presence of electrostatic potential. The electrons are accelerated around the X line and then turned to the outflow direction by the Lorentz force, and the electrostatic potential acts to counteract this turning process. In our simulations, for ions, the electric field force and the Lorentz force are almost comparable within the inner EDR region, accelerating ions to form an ion outflow. In the outer EDR and the downstream region, the Lorentz force is much larger but almost completely balanced by the pressure gradient force, and the influence of the electric field force on ion acceleration cannot be ignored. For electrons, both the electric field force and the pressure gradient force can balance the Lorentz force. The pressure gradient force in the inner EDR region is slightly larger than the electric field force. This may be related to the initial electron temperature set in our simulations, which requires further investigation.