Evaluation of influence of detrending CSES satellite data on lithospheric magnetic field modeling

1.   Introduction

Lithospheric magnetic anomalies quickly decrease with the altitude, and only a few magnetic anomalies with a long wavelength can still be detected onboard low-Earth-orbit satellites. Satellite magnetic anomalies are generated by large-scale magnetized rocks in the crust and locally, the uppermost mantle of the Earth (Ferré et al., 2014). Their geological origins are generally related to plate tectonics, lower crustal processes and impacts, and they reflect important information on the constitution, structure, and evolution of the crust (Purucker and Clark, 2011; Wang J et al., 2024a, b).

The American POGO (1967–1971) and Magsat (1979–1980) satellites confirmed that weak lithospheric magnetic anomalies are detectable on satellite, and generated maps of the global magnetic anomalies (Regan et al., 1975; Langel and Hinze, 1998; Arkani-Hamed et al., 1994). The Danish Ørsted (1999–2013) and German CHAMP (2000–2010) satellites provided particularly valuable data over a long period that helped develop lithospheric magnetic field modeling (Maus et al., 2002, 2007; Purucker et al., 2002; Sabaka et al., 2015). The ESA’s Swarm satellite constellation (2013–) has been designed specifically for geomagnetic field monitoring, and its data have further improved the spatial resolution of satellite-based models of the lithospheric magnetic field (Olsen et al., 2017). China has launched two satellites with the capability of magnetic detection — the China Seismo-Electromagnetic Satellite (CSES; 2018–) and the Macao Science Satellite-1 (MSS-1; 2023–). Data from the CSES have been used to derive a global model of the lithospheric magnetic field (Wang J et al., 2023a).

The lithospheric magnetic field has been modeled based on data from the CSES (Wang J et al., 2023a) by using a serial approach (Thébault et al., 2010), whereby the contributions of all other magnetic fields are sequentially eliminated by using an a priori model. However, in spite of the stringent procedures for data selection (Kauristie et al., 2017) in this sequential approach, residual signals or perturbation fields persist in the data (Finlay et al., 2017) mainly owing to the dynamic system created by the coupling of solar wind, the magnetosphere, ionosphere, and core internal magnetic fields (Thébault et al., 2017). Following the removal of the core and external fields by using the CHAOS-7 model (Finlay et al., 2020), prominent residual trends persisted within the along-track data on magnetic anomalies of the CSES. However, no processing was undertaken to deal with these residual trends to avoid subjective processing and represent the realistic nature of the data. In general, residual signals are filtered by using methods of along-track external field correction, such as Fourier filtering, polynomial filtering, high-pass spherical harmonics, singular spectral analysis, and line levelling (Thébault et al., 2012, 2017; Lesur et al., 2013). These residual signals may be introduced to the model of the lithospheric magnetic field if they are not suitably dealt with. In this work, we analyze the influence of the residual trends on lithospheric magnetic field modeling and provide suggestions on detrending the data.

2.   Background

2.1   Orbital Information and Magnetic Data of CSES

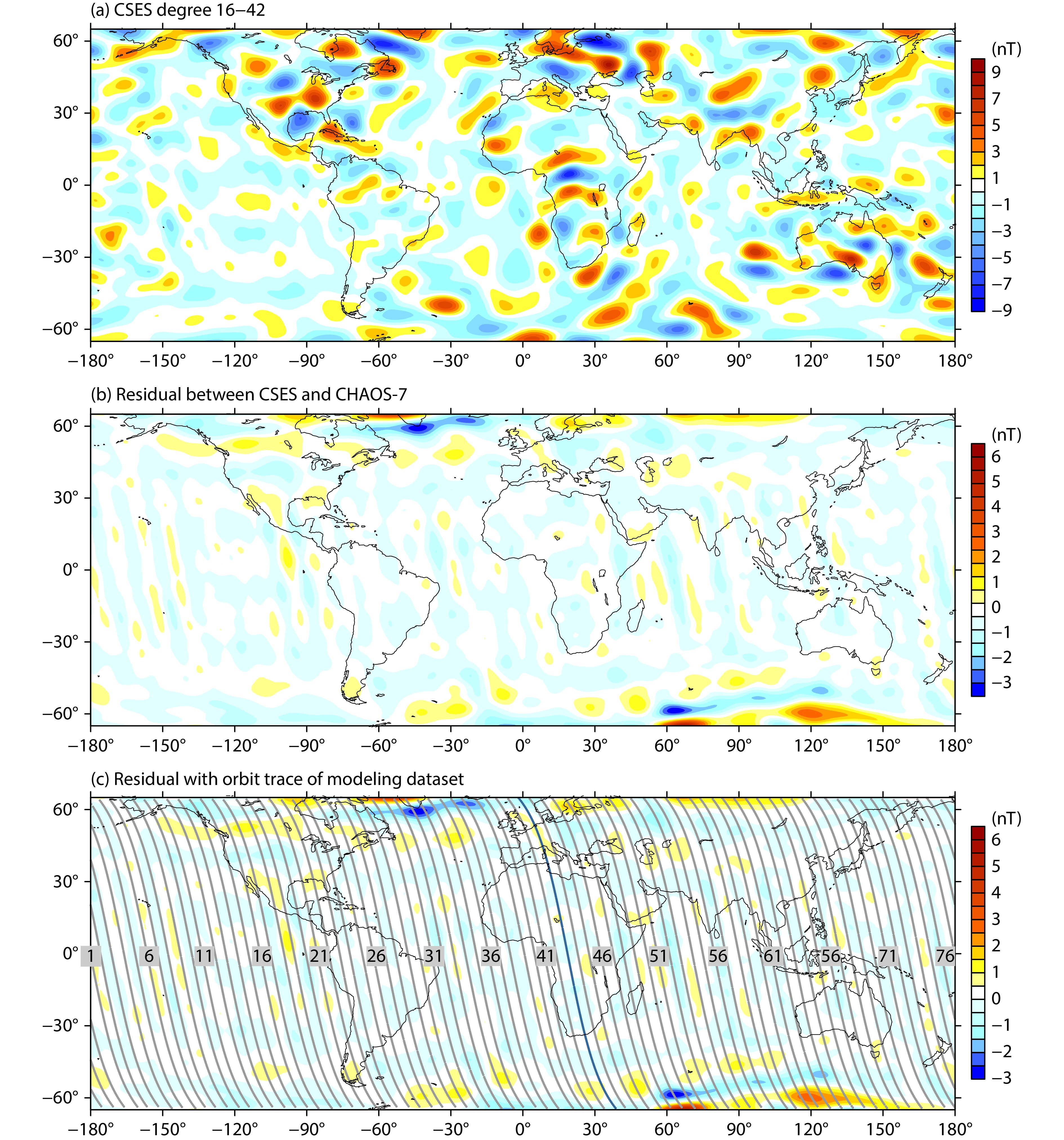
The CSES satellite was launched in February 2018. It was designed to measure geophysical fields for research on space and solid earth physics (Shen XH et al., 2018; Zeren ZM et al., 2024). The CSES is on a nearly circular, near-polar, sun-synchronous orbit at an inclination angle of 97.4°. It revisits each orbit every five days, and flies at a mean altitude of 507 km above a sphere of radius 6371.2 km. It requires 76 orbits for global coverage, and each can be divided into two half-orbits: night-side (ascending node at local time 02:00) and day-side orbits (descending node at local time 14:00). Traces of the night-side orbit are shown in Figure 1c, and the orbits are numbered after every five orbits.

Figure  1.  (a) Map of lithospheric magnetic anomalies calculated by the CSES model at 500 km. (b) Residuals between the CSES and CHAOS-7 models. (c) 76 orbital traces of night-side data obtained by the CSES. The base layer is identical to that shown in Figure 1b. Modified from Wang J et al. (2023a).

DownLoad: Full-Size Img PowerPoint

The high precision magnetometer (HPM) onboard the CSES carries two fluxgate magnetometers (FGM, Zhou B et al., 2019) for vector measurements, as well as a coupled dark-state magnetometer (CDSM, Pollinger et al., 2020) for scalar measurements at a sampling rate of 1 Hz. The CDSM has an accuracy of 0.19 nT (Pollinger et al., 2018). An on-ground prelaunch test showed that remaining magnetic interference from the platform at the center of the CDSM sensor was lower than 0.33 nT (Cheng BJ et al., 2018). The quality of the data captured by the HPM data has been confirmed (Yang YY et al., 2021a; Zeren ZM et al., 2022), and they can be downloaded from https://leos.ac.cn. They have been used for the modeling of the geomagnetic core field (Yang YY et al., 2021b) as well as lithospheric magnetic field (Wang J et al., 2021, 2023a, b).

2.2   Global Lithospheric Magnetic Field Model Derived from CSES Data

Scalar magnetic data from the CSES have been used to derive a global model of the lithospheric magnetic field between the geographic latitudes of ±65° (Wang et al., 2023a). The coefficients of the model are available at https://www.leos.ac.cn/#/article/info/250. We chose night-side data from March 2018 to November 2022 under quiet space weather conditions. We then removed the core and external fields by using the CHAOS-7 model (Finlay et al., 2020). After further data quality control, we used them to build a lithospheric magnetic field model through spherical harmonic (SH) analysis. The CSES model thus obtained was compared with other important models in terms of the power spectrum and details of the anomalies. The results confirmed that scalar data from the CSES can provide a reliable model of the lithospheric magnetic field for up to SH degree 42. Figure 1 shows the map of the lithospheric magnetic anomalies, calculated by using the CSES model at 500 km, as well as the residuals compared with the CHAOS-7 model. The residuals were mostly detected along the orbit of the satellite and were caused by the gridding of a discrete dataset with large spaces in the survey line. The orbital interval of the CSES satellite was relatively large, which is 360°/76 (circles for a global coverage) ≈ 4.7°, and the residuals in the orbital gap were larger than those along the orbit. This was especially prominent in low-latitude areas, as shown in Figure 1c.

2.3   Trend of Magnetic Anomalies in CSES Data

After removing the core and external fields, the magnetic anomalies exhibited a residual trend that could be represented by the along-track mean value. We calculated the mean values of magnetic anomalies in the datasets for each orbit, and the orbit numbers shown in Figure 2a are identical to those in Figure 1c. The mean values for different orbits varied and most of them were positive. The mean value of the entire dataset was 0.904 nT.

Figure  2.  The mean values of (a) the CSES dataset for lithospheric magnetic field modeling, and (b) Orbit 43 across the Bangui magnetic anomaly at 5° latitude.

DownLoad: Full-Size Img PowerPoint

To clearly show the trend of magnetic anomalies in CSES data, we chose data on Orbit 43, which was across the famous Bangui magnetic anomaly — a prominent, low magnetic signal at 5° N latitude. A total of ninety-three revisited files for Orbit 43 have been analyzed, yielding a mean observation value of 1.849 nT, the estimation along Orbits 43, derived from the CSES lithospheric magnetic field model, is calculated to be 0.244 nT. The mean value of estimates of the model was close to zero, while the difference between the observed and estimated values indicates that there was a residual trend in the observations owing to non-lithospheric magnetic sources.

2.4   Source of Trend in CSES Data

The residual trends in the data on magnetic anomalies from the CSES reflected signals from non-lithospheric magnetic sources. Because the lithospheric magnetic field originates from magnetized rocks in the crust and locally uppermost mantle of the Earth (Ferré et al., 2014), these signals are relatively stable. The residual trends might have had three possible sources: (1) remaining influence of the external field, (2) difference in satellite platforms, and (3) time-variable component of the lithospheric magnetic field. As changes in the lithospheric magnetic field were minimal during this study, they were ignored, and sources (1) and (2) above were identified as the main cause of the residual trend.

Figure 2b shows that the residual trend in each track was different, which means that it was a variable component, and this is consistent with the properties of the external field. The external field was removed before modeling by using the CHAOS-7 model, and the residual trends were mostly caused by the part of the external field that the model failed to fit. This part originated from the dynamic system created by the coupling between solar wind, the magnetosphere, ionosphere, and core internal magnetic fields (Thébault et al., 2017).

Another possible source of the residual trends might have been the difference between the satellite platforms. The data on the core field were also removed by using the CHAOS-7 model. The latter was derived from data from the Ørsted, CHAMP, SAC-C, CryoSat-2 and Swarm satellites, and did not include data from the CSES. The mean values of the CHAOS-7 model for non-polar data from these satellites are listed in Table 1 (Finlay et al., 2020). The amplitudes of misfits of data from the Ørsted and CHAMP satellites both exceeded 0.5 nT, while those of the SAC-C, CryoSat-2, and Swarm were relatively small, and no greater than 0.1 nT. This implies that there were intrinsic differences among the data from different satellites that were possibly caused by the use of inconsistent platforms and instruments.

Table  1.  Misfits between non-polar satellite data and the CHAOS-7 model. (Data from Finlay et al., 2020).

Satellite	Mean (nT)	Satellite	Mean (nT)
Ørsted	0.53	Swarm-A	$-$0.07
CHAMP	$-$0.53	Swarm-B	$-$0.07
SAC-C	0.10	Swarm-C	0.00
CryoSat-2	0.02

 | Show Table

DownLoad: CSV

3.   Methodology

3.1   Spherical Harmonic (SH) Modeling

The potential $V$ of the internal magnetic field $\boldsymbol{B}=-\nabla V$ satisfies Laplace’s equation. The solution of Laplace’s equation can be expressed in the geocentric spherical coordinate system by a series of spherical harmonics:

where $a=6371.2$ km is the Earth’s mean radius, $(r,\theta ,\phi )$ represent the radius, colatitude, and longitude, respectively, in geocentric spherical coordinates, ${g}_{n}^{m}$ and ${h}_{n}^{m}$ are Gaussian spherical harmonic coefficients, N is their maximum degree, and ${P}_{n}^{m}$ is the associated Schmidt semi-normalized Legendre function.

SH modeling is to estimate the Gaussian coefficients, which is equivalent to obtaining the solution to linear equations. We used the LSQR algorithm (Paige and Saunders, 1982), which is integrated into MATLAB^®, to solve the large, overdetermined linear equations. This algorithm uses a damped iterative method to reliably solve ill-conditioned linear equations.

The dataset and method for modeling were the same as for the CSES original model. For detailed information on lithospheric magnetic field modeling, the interested reader can refer to Wang J et al. (2023a).

3.2   Along-track Detrending by Using Polynomials

Because the residual trends vary gently in low-order terms, we used polynomials to fit the trend of each track and remove it to detrend the data. We used 0-order, 1-order, 2-order, and 3-order polynomials for along-track detrending to evaluate its influence on modeling. They can be expressed as follows:

0-order (constant) polynomial: $y={a}_{0}$,

1-order (linear) polynomial: ${y=a}_{0}+{a}_{1}x$,

2-order (quadratic) polynomial: ${y=a}_{0}+{a}_{1}x+{a}_{2}{x}^{2}$,

3-order (cubic) polynomial: ${y=a}_{0}+{a}_{1}x+{a}_{2}{x}^{2}+{a}_{3}{x}^{3}$.

In the above, y corresponds to the trend of fitting, x represents the latitude of each track, and ${a}_{0},{a}_{1}{,a}_{2},{a}_{3}$ are the polynomial coefficients. Figure 3 shows the fitted trends and anomaly data obtained after detrending single-track data for Orbit 43 across the Bangui magnetic anomaly by using polynomials of different orders.

Figure  3.  (a) Fitted trends obtained by using the polynomials, and (b) anomaly data obtained after detrending data on Orbit 43. This single-track data across the Bangui magnetic anomaly were obtained on June 23, 2020 (track number 132511).

DownLoad: Full-Size Img PowerPoint

4.   Results and Discussion

4.1   Detrending Models in Grid Maps

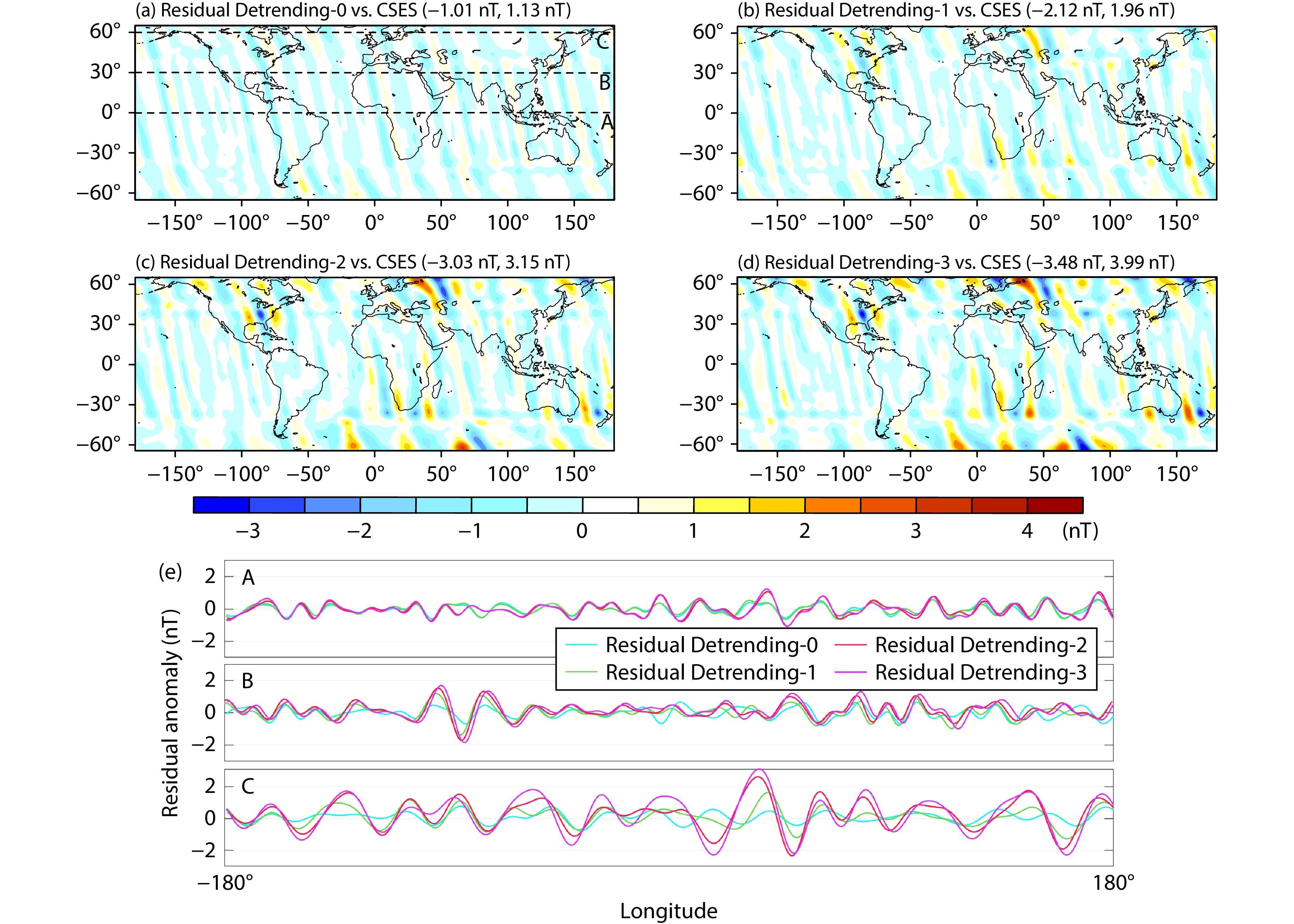
The dataset used for modeling was the one used for the CSES original model (Wang J et al., 2023a). After detrending the data by using polynomials, we applied them to derive four models of the lithospheric magnetic field — Detrending-0, Detrending-1, Detrending-2, and Detrending-3 — corresponding to the modeling datasets detrended by using polynomials of orders 0–3, respectively. Table 2 lists the statistics of the CSES original model and the detrending models, including the misfits, range of field values, residuals compared with the CHAOS-7 model, and the residuals between the CSES original model and the four detrending models.

Table  2.  Statistics of the CSES original model and the detrending models.

Model	Misfit (nT)	Field value (nT)	Residual with CHAOS-7 (nT)	Residual with CSES original (nT)
CSES original	0.0019	(−8.52, 8.39)	(−2.90, 5.75)	−
Detrending-0	0.0013	(−8.83, 7.74)	(−3.29, 5.31)	(−1.01, 1.13)
Detrending-1	0.0010	(−8.91, 7.27)	(−3.04, 5.81)	(−2.12, 1.96)
Detrending-2	0.0007	(−7.89, 7.57)	(−3.95, 8.43)	(−3.03, 3.15)
Detrending-3	0.0006	(−7.91, 7.44)	(−4.34, 8.14)	(−3.48, 3.99)

 | Show Table

DownLoad: CSV

The misfits between the results of model estimation and the datasets are listed in Table 2. The misfits of all models were minor, with the CSES original model yielding a misfit of 0.0019 nT. As the order of the polynomials increased, the misfit of the detrending models decreased. The misfit of the Detrending-3 model was only 0.006 nT, indicating improved fitting after introducing detrending for the datasets.

Figure 4 illustrates maps of the lithospheric magnetic anomalies and their residuals with the CHAOS-7 model, with a 0.5° × 0.5° grid calculated by the CSES original model and the four detrending models at an altitude of 500 km. The ranges of values of these models and the residuals are listed in Table 2. The maximum values of the detrending models generally decreased with the order of the polynomial used, which means that detrending reduced the amplitude of the datasets. The Detrending-1 model obtained the lowest value, and its maximum value decreased to 7.27 nT, while those of the Detrending-2 (7.57 nT) and Detrending-3 (7.44 nT) models were higher. However, this does not reflect an increase in the power spectra of the Detrending-2 and Detrending-3 models. This is because the amplitude of the residuals also increased with the order of the polynomials. The maximum values of the residuals for the Detrending-2 and Detrening-3 models were 8.43 and 8.14 nT, respectively, which exceeded even their respective maximum values of 7.57 and 7.44 nT. Therefore, the observed increase in value for Detrending-2 and Detrending-3 model may be attributed to detrending processing itself, which altered the data value rather than indicating an actual enhancement of the signal strength.

Figure  4.  CSES lithospheric magnetic anomaly maps derived from detrending models and residuals with CHAOS-7 model in degree 16$-$42 at 500 km altitude.

DownLoad: Full-Size Img PowerPoint

4.2   Comparison Between CSES Original Model and Detrending Models

The detrending models were compared with the CSES original model in terms of the distribution of the residuals and the power spectrum. Figure 5 shows a grid map of the comparison of their residuals. Three profiles of anomalies in the east–west residuals were identified in the four detrending models along latitudes 0°, 30°, and 60°. As the order of the polynomials increased, so did the magnitude of the residuals, indicating a greater change in the dataset. The 0- and 1-order polynomials were both straight lines, and the corresponding changes in the dataset were relatively limited. However, the 2- and 3-order polynomials were characterized by curves, and the corresponding changes in the dataset were large, particularly in the high-latitude region that was more severely influenced by external fields. Moreover, there were two prominent distorted signals nearly along 40° N and 40° S. They were obtained because we conducted the data quality control at low latitudes (|latitude| ≤ 40°) and high latitudes (40° < |latitude| < 65°) separately during modeling. This led to the elimination of data containing severe interference at high latitudes, and the resulting edge effect led to worse fitting at 40° latitude.

Figure  5.  (a)–(d) Maps of residuals between the four detrending models and the CSES original model at SH degree 16–42 at an altitude of 500 km. (e) Three profiles of anomalies in the east–west residuals in the four detrending models along latitudes 0°, 30°, and 60°. Their locations are shown in Figure 5a.

DownLoad: Full-Size Img PowerPoint

Figure 6a shows a comparison of power spectra between the CSES original model and the four detrending models at SH degree 1–42. In the range of SH degree 1–15, the inverted coefficients were not zero and were more sensitive to detrending-related processing than those at larger degrees. We removed the core field to SH degree15, and set the coefficients below degree 16 to zero to avoid uncertainty in the results of fitting of low-degree terms. The power of the detrending models was lower than that of the CSES original model, and continued to decrease as the order of the polynomials increased. Figure 6b shows the differences in the power spectrum obtained by subtracting those of the detrending models from that of the CSES original model. It more clearly shows the reduction in power. This reveals that the strength of the signal decreased when interference by the residual trend was suppressed during the detrending of the data. The reduction in signal strength was more significant for detrending models that used higher-order polynomials.

Figure  6.  Comparison between the four detrending models and the CSES original model in terms of the (a) power spectrum and (b) difference in power spectrum.

DownLoad: Full-Size Img PowerPoint

4.3   Iterative Convergence of SH Coefficients

We estimated the SH coefficients of the CSES dataset by using the LSQR algorithm over 60 iterations. Figures 7a–e illustrate the Lowes–Mauersberger power spectra (Mauersberger, 1956; Lowes, 1966) of the CSES original model and the four detrending models under different times of iterations.

Figure  7.  The SH coefficient convergence, represented by the (a)–(e) power spectra and (f)–(j) SH correlation analysis of the CSES original model and the four detrending models under different times of iterations.

DownLoad: Full-Size Img PowerPoint

The power spectrum of the CSES models showed that their results were consistent under different times of iterations until SH degree 42. Above degree 42, the differences in the power spectra of the models under different times of iterations increased prominently such that their results became unreliable. We thus truncated the CSES original model at degree 42 (red dashed line) and used the results obtained after 40 iterations.

After detrending the data, the convergence of the power spectrum improved significantly under different times of iterations, and the results remained highly consistent until degree 44. To quantitatively measure the consistency of the results under different times of iterations, Figures 7f–j show the SH correlation analysis between the model run for 40 iterations and those iterated for different times of iterations. The SH correlation between the CSES original model when run for 20 and 60 iterations was 0.93 at degree 42, while it was greater than 0.96 after detrending the data. The convergence of the model did not further improve with an increase in the order of the polynomials.

4.4   Comparison of Regional Details

To further evaluate the detrending models, we compared their regional details with those of the CSES original model and the CHAOS-7 model. Figure 8 shows the magnetic anomalies in the Himalayan–Tibetan Plateau and surrounding regions, obtained at an altitude of 500 km, as calculated by the CSES original model, CHAOS-7 model, and the four detrending models. The southern Himalayan–Tibetan Plateau features an east–west-trending magnetic low anomaly (HMLA), and there is another significant high magnetic anomaly in the Tarim Basin (TMA) to the north. The distributions of these magnetic anomalies obtained by all models were similar, but there were prominent differences in their details. We provide some examples below.

Figure  8.  (a)–(f) Regional magnetic anomalies of different models, and (g)–(j) residuals between the four detrending models and the CHAOS-7 model in the Himalayan–Tibetan Plateau and surrounding areas.

DownLoad: Full-Size Img PowerPoint

HMLA: The HMLA appeared as three separate low magnetic anomalies lined up in an east–west direction in the CSES original model. However, the HMLA tended to be connected as a single anomaly in the CHAOS-7 model and the detrending models, indicating that the discontinuity in the CSES original model might have been related to the residual trends, and that the detrending had improved the consistency of data from different orbits. But from Detrending-1 model, the spatial area of HMLA decreases.

TMA: The shape of the TMA changed significantly between the Detrending-2 and -3 models, and the latter contained serious distortions. The center of the TMA in it had a prominent northward offset, indicating that detrending had introduced a large deviation in the magnetic anomaly.

5.   Conclusions

In this study, we used polynomial fitting to remove the residual trend of data on magnetic anomalies obtained from the CSES satellite, and used polynomials of orders 0 to 3 to derive four detrending models. The aim was to identify the influence of the residual trends on modeling. We compared the detrending models with the CSES original model in terms of the power spectrum and grid maps. The following conclusions can be drawn:

(1) Positive aspect of detrending: After detrending, the misfit between the model and the dataset decreased, and the convergence of the SH coefficients improved.

(2) Negative aspect of detrending: Detrending led to a reduction in signal strength and a decline in the power spectrum. Detrending based on polynomials of orders 2 and 3 introduced prominent distortions in the details of the anomalies.

(3) Suggestion on detrending: We recommend detrending the data on magnetic anomalies obtained by the CSES before modeling, but by using only 0-order polynomials, i.e., subtracting a constant value to reduce the mean value of the magnetic anomaly to zero. This will lead to only a slight loss of signal strength in return for a significant improvement in the stability of the coefficient and details of the anomalies. Further analysis of the sources of residual signals in different satellites and more advanced methods of detrending are needed to provide a comprehensive strategy for dealing with residual trends.