Influence of upstream solar wind on magnetic field distribution in the Martian nightside ionosphere

1.   Introduction

Approximately 3.5 billion years ago Mars was warm and habitable, with a considerably thick atmosphere (Jakosky and Phillips, 2001; Carr and Head III, 2003; Jakosky et al., 2017). Currently, the Martian atmosphere is thin; the majority of its earlier atmospheric components long ago escaped into space. It is recognized that planetary ions escape to interplanetary space through electromagnetic forces and associated particle dynamic processes (e.g., Barabash et al., 2007; Lundin, 2011; Futaana et al., 2017; Zhang C et al., 2022). Therefore, understanding in detail the magnetic field distribution in the Martian atmosphere is crucial to constrain the process of planetary particle escape and ultimately to understand the evolution of Martian habitability (e.g., Connerney et al., 2015a; Ramstad and Barabash, 2021).

Unlike Earth, Mars lacks a global dipolar magnetic field; the planet does have locally distributed crustal magnetic fields (Acuña et al., 1999; Gao JW et al., 2021; Mittelholz and Johnson, 2022). Mars is exposed to the solar wind, which carries the Interplanetary Magnetic Field (IMF) that interacts with Mars’ highly conductive ionosphere, resulting in an induced magnetosphere (Luhman et al., 2004). The IMF drapes around the ionospheric obstacle, appears “hung up” in the dayside, and is stretched by the solar wind to form an induced magnetotail (e.g., Luhmann et al., 2004; Brain et al., 2017).

Over the past two decades, NASA’s Mars Global Surveyor (MGS) and the Mars Atmosphere and Volatile EvolutioN (MAVEN) spacecraft have extensively measured the Martian magnetic field at atmospheric altitudes. The MGS spacecraft, providing the first comprehensive magnetic field measurements at Mars, mainly sampled at an altitude of 400 km. The Martian magnetic field comprises both induced and crustal magnetic fields (Connerney et al., 1999; Brain et al., 2003). At the nightside, it has been determined that the predominant contributor to the weak external magnetic field is the draping of the IMF, which can extend to about 400 km altitude (Ferguson et al., 2005; Mittelholz et al., 2017). These findings suggest the presence of a magnetotail-like feature down to ionospheric altitudes on Mars’ nightside (Ferguson et al., 2005). However, MGS was unable to measure the induced magnetic field at such lower altitudes as 100−200 km. In 2014, the MAVEN mission became the first spacecraft to routinely measure low-altitude Martian magnetic fields at varying local times. Analysis of MAVEN data revealed that the penetration of the draped magnetic field into the dayside Martian ionosphere can reach down to 150−200 km altitude (Fowler et al., 2019; Huang JP et al., 2023; Fang XH et al., 2023). When draped magnetic field lines penetrate into atmospheric altitudes, they create a planetary escape channel for charged ionospheric particles (Xu SS et al., 2017; Fowler et al., 2019; Shuvalov et al., 2024).

An intriguing aspect of this emerging scenario is the question: How do variations in upstream solar wind conditions impact the topology of the low-altitude induced magnetic field on Mars (Brain et al., 2020; Fang XH et al., 2023; Fowler et al., 2024)? The induced field topology exhibits statistical variation in response to solar conditions, such as the IMF’s strength and direction, solar wind dynamic pressure (${P}_{{\mathrm{SW}}}$), and solar extreme ultraviolet (EUV) flux, which vary with solar seasons. It is broadly recognized that the induced magnetosphere, on both the dayside and nightside, compresses under high solar wind pressure conditions (Luhmann et al., 1980; Luhmann et al., 1981; Weber et al., 2019), facilitating deeper IMF penetration during these periods. Additionally, Brain et al. (2020) suggested that during periods of high EUV, the increase in photoionization enhances ionospheric thermal pressure on the dayside and near the terminator, which in turn inhibits the penetration of the draped IMF into the ionosphere. Given that the historical solar wind is believed to have been denser and faster than today’s conditions (Kulikov et al., 2007), normal solar wind conditions in the past may have resembled today’s extreme dynamic pressure events, such as those during coronal mass ejections (CMEs) and in co-rotating interaction regions (CIRs) (Curry et al., 2015; Luhmann et al., 2017; Xu SS et al., 2017; Luo H et al., 2022). Depending on the solar conditions experienced by Mars in the past, the draped magnetic field may have routinely penetrated deep into the ionosphere, potentially leading to significantly higher rates of ionospheric escape to space for early Mars compared to the present day (Fowler et al., 2019). Therefore, understanding how solar conditions influence the Martian ionospheric magnetic field, especially the penetration depth of the IMF, is crucial for elucidating the past history of Mars’s ion escape processes. However, the influence of upstream solar conditions, such as the intensity of the IMF, solar wind dynamic pressure, solar extreme ultraviolet flux, and Martian seasons, on the nightside magnetic field distribution in the Martian ionosphere has yet to be quantitatively determined. Furthermore, understanding the distribution of the nightside magnetic field at low altitudes is essential for distinguishing between the internal and external components of the Martian magnetic field, which is essential to accurate modeling of the planet’s crustal magnetic field.

Here, we present a statistical analysis based on over eight years of magnetic field observations from the MAVEN mission, spanning from November 2014 to May 2023, to investigate the impact of solar conditions on the external magnetic field distribution in the Martian nightside ionosphere. Our study focuses primarily on how various solar conditions affect the penetration depth of the IMF into the nightside ionosphere. The aims of this study are to enhance our understanding of the magnetic field environment under varying solar conditions. Moreover, this study can also provide important constraints on removing the influence of external fields in order to improve accurate modeling of Mars’ internal, crustal magnetic field. In Section 2, we provide an overview of the MAVEN dataset and the coordinate system utilized. Section 3 presents our findings; conclusions and discussion appear in Section 4.

2.   Data and Coordinates

This study utilizes MAVEN magnetic field and plasma measurements (Jakosky et al., 2015). Launched in September 2014, MAVEN orbits Mars in an elliptical trajectory with initial periapsis and apoapsis altitudes of 150 km and 6000 km, respectively. The apoapsis altitude was adjusted to 4400 km after an aerobraking maneuver in 2019. At ionospheric altitudes, MAVEN spans from 150 km to 600 km at all local times; it also can collect limited lower altitude data down to 110 km. Magnetic field data were measured by the fluxgate magnetometers (MAG) aboard MAVEN, with the vector magnetic field data being resampled at 4 s intervals to filter out high-frequency wave signals (Connerney et al., 2015b). Upstream solar wind velocity and density were measured by the Solar Wind Ion Analyzer (SWIA) instrument, which measures ion fluxes within an energy range of 25 eV to 25 keV, with a time resolution of 4 s (Halekas et al., 2015).

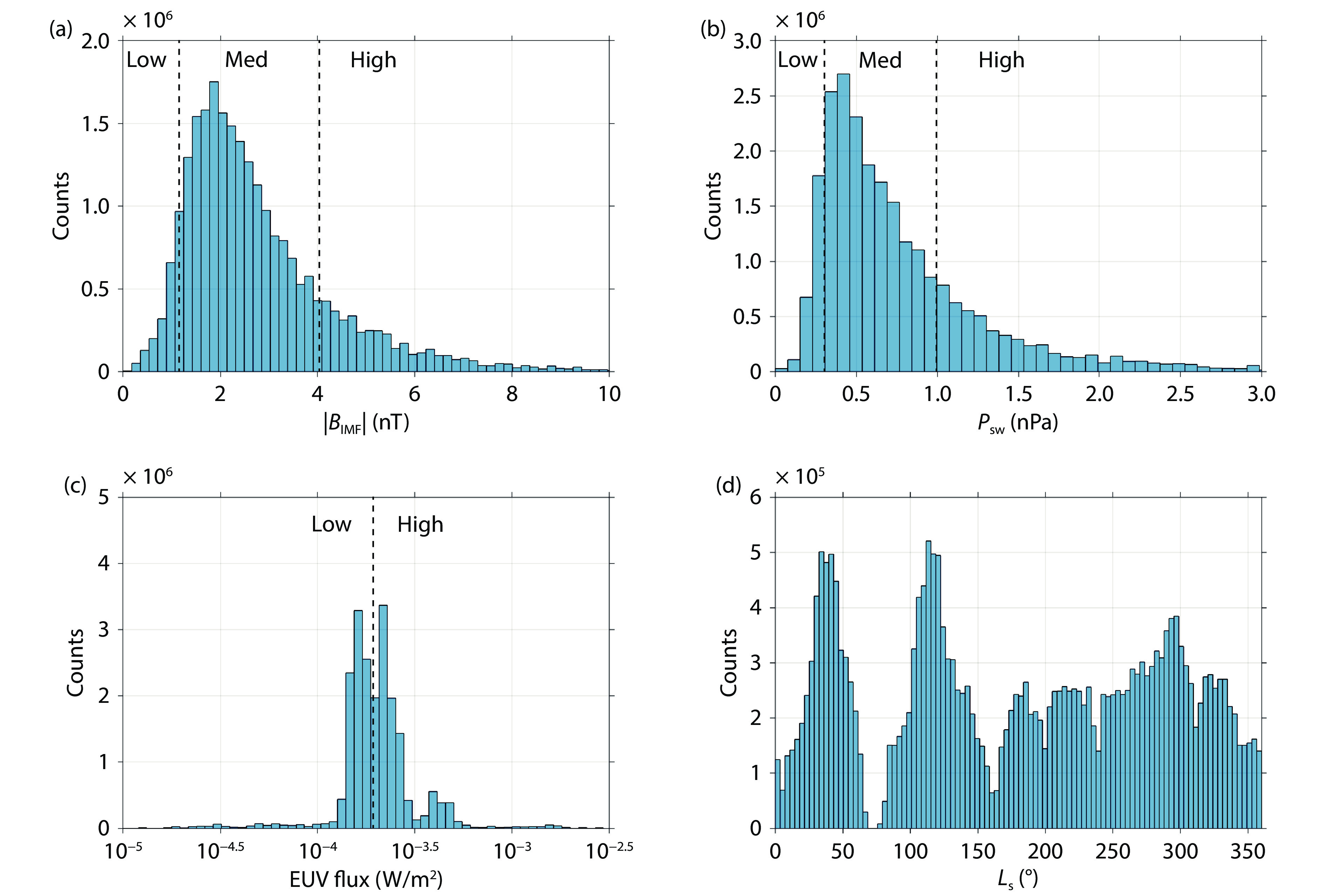
To evaluate upstream solar wind conditions for each orbit, orbits were chosen when MAVEN was adequately distant from the Martian bow shock, specifically when the apoapsis was positioned 0.3 ${R}_{{\mathrm{m}}}$ away from a bow shock model (Trotignon et al., 2006). Bow shock crossings were manually identified by Gao JW (2021), similar to methods employed in previous studies (Gruesbeck et al., 2018; Liu D et al., 2021). We further specified that the solar wind interval between neighboring bow shock crossings should exceed 1.5 hours, resulting in data from a total of 6846 orbits from November 2014 to May 2023. For each such orbit, solar wind parameters were averaged within a 30-minute window centered around the apoapsis, and these averaged parameters were subsequently applied across the entire orbit. We examined the influence of the IMF intensity ($\left|{\boldsymbol{B}}_{{\mathrm{IMF}}}\right|$), solar wind dynamic pressure (${P}_{{\mathrm{SW}}}$), the solar extreme ultraviolet (EUV) flux, and the Martian season (Mars solar longitude ${L}_{{\mathrm{s}}}$) on Martian external magnetic field distribution at ionospheric altitudes. The ${P}_{{\mathrm{SW}}}$ is calculated as ${P}_{{\mathrm{SW}}} = nm{V}^{2}$, where $n$ is the solar wind density, $m$ is proton mass, and $V$ is the solar wind velocity. The EUV flux is measured by MAVEN’s EUVM instrument (Eparvier et al., 2015). We utilized EUVM Level 2 data in the Channels A (17−22 nm), which measures solar irradiance from the non-flaring corona (Thiemann et al., 2017; Lillis et al., 2021).

In this study, the magnetic field is analyzed in the Mars−Solar−Orbital (MSO) coordinate system, where ${+X}_{{\mathrm{MSO}}}$ points toward the Sun, ${+Y}_{{\mathrm{MSO}}}$ is antiparallel to the Mars orbital velocity, and ${+Z}_{{\mathrm{MSO}}}$ completes the right-handed coordinate system. Unless otherwise stated, the location of the dayside (nightside) is defined as where the solar zenith angle of the location is <90° (>90°), respectively. In the MSO coordinate, the MAVEN data coverage spans all latitudes and longitudes without significant gaps (see Figure 1a). In examining the external magnetic field distribution and aiming to exclude the influence of the crustal field, we selected data points from non-crustal field regions, analyzed in Planetocentric (PC) coordinates as shown in Figure 1b. The PC coordinates are orthogonal Cartesian coordinates, rotating with the Mars body. Data from non-crustal field regions were selected only when magnetic field amplitudes were below 5 nT, as evaluated at the observation location using a crustal field model (Gao JW et al., 2021). Additionally, the north-south asymmetry in data coverage indicates that data were collected primarily in the Northern Hemisphere.

Figure  1.  MAVEN data distribution in the Martian ionosphere in Mars−Solar−Orbital (MSO) and Planetocentric (PC) Coordinates. (a) Distribution of MAVEN data in MSO coordinates, measured below 600 km altitude. (b) Distribution of MAVEN data in non-crustal field regions in Planetocentric (PC) coordinates. The black contours delineate the intensity of the crustal magnetic field at 120 km altitude, from the crustal field model (Gao JW et al., 2021).

DownLoad: Full-Size Img PowerPoint

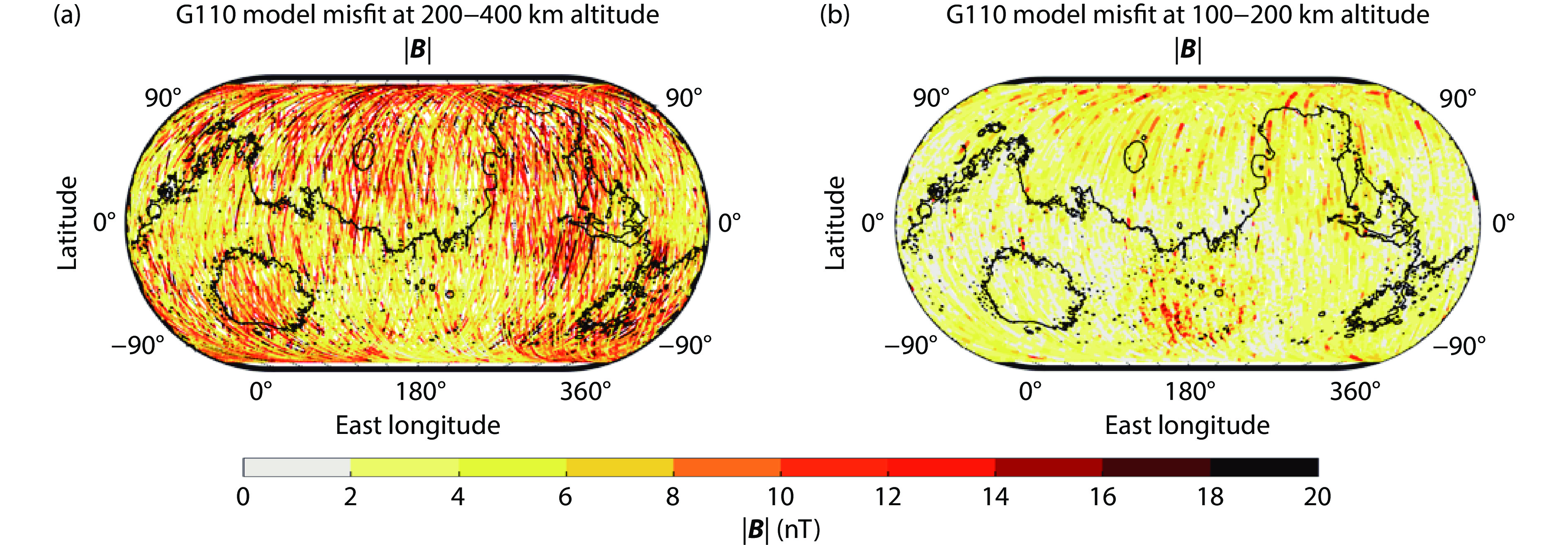
Magnetic field residuals were further determined by subtracting a crustal field model from the observed magnetic field measurements (Gao JW et al., 2021). These residuals are interpreted as magnetic field contributions driven by the IMF and ionosphere. Figure 2 demonstrates that, within the MAVEN data set, the residuals of the G110 model at altitudes of 200–400 km are more pronounced in regions with weak crustal fields than in those with strong crustal fields (Gao JW et al., 2021). This distribution suggests that the residuals are influenced predominantly by external magnetic fields rather than internal magnetic fields. Consequently, these magnetic field residuals can be considered as reflective of the external magnetic field. While this method substantially mitigates the direct influence of the crustal field on the external magnetic field contribution, it may not fully eliminate indirect influences of ionospheric currents on the crustal field regions (Riousset et al., 2014).

Figure  2.  Map of the residual magnetic fields from the G110 crustal magnetic field model for the MAVEN data set, showing altitudes (a) between 200 and 400 km and (b) between 100 and 200 km (adapted from Gao JW et al., 2021).

DownLoad: Full-Size Img PowerPoint

3.   Results

We have investigated variations in the nightside magnetic field distribution in response to four distinct upstream drivers: the intensity of the IMF (${{\boldsymbol{B}}}_{{\mathrm{IMF}}}$), solar wind dynamic pressure (${P}_{{\mathrm{SW}}}$), the solar extreme ultraviolet (EUV) flux, and Martian season (${L}_{{\mathrm{s}}}$). Figure 3 presents histograms for each driver in the value range utilized in this study. Considering the wide variation in upstream $\left|{{\boldsymbol{B}}}_{{\mathrm{IMF}}}\right|$ and ${P}_{{\mathrm{SW}}}$, we categorize the measurements into low, medium, and high segments for both $\left|{{\boldsymbol{B}}}_{{\mathrm{IMF}}}\right|$ and ${P}_{{\mathrm{SW}}}$, as indicated in Figure 3. In this study, unless otherwise stated, the categorization of $\left|{{\boldsymbol{B}}}_{{\mathrm{IMF}}}\right|$ is defined as: <1 nT for low $\left|{{\boldsymbol{B}}}_{{\mathrm{IMF}}}\right|$, 1−4 nT for medium $\left|{\boldsymbol{B}}_{{\mathrm{IMF}}}\right|$, and >4 nT for high $\left|{\boldsymbol{B}}_{{\mathrm{IMF}}}\right|$. Similarly, for ${P}_{{\mathrm{SW}}}$, the categories are: <0.3 nPa for low ${P}_{{\mathrm{SW}}}$, 0.3−1 nPa for medium ${P}_{{\mathrm{SW}}}$, and >1 nPa for high ${P}_{{\mathrm{SW}}}$; these choices are consistent with the criteria used in previous studies (Brain et al., 2020). Additionally, we divide the dataset based on EUV radiation levels, using a threshold set at $2\times {10}^{-4}$ ${{\mathrm{W/m}}}^{2}$ to distinguish between low and high EUV conditions.

Figure  3.  Histograms of MAVEN low altitude (<600 km) measurements of (a) intensity of IMF ($\left|{\boldsymbol{B}}_{{\mathrm{IMF}}}\right|$), (b) solar wind dynamic pressure (${P}_{{\mathrm{SW}}}$), (c) EUV flux, and (d) Martian season (${L}_{{\mathrm{s}}}$). The histograms of $\left|{\boldsymbol{B}}_{{\mathrm{IMF}}}\right|$ and ${P}_{{\mathrm{SW}}}$ are divided into three subsets, corresponding to the low, medium, and high solar driver defined in this study. The EUV flux is categorized into two subsets, reflecting different levels of solar irradiance.

DownLoad: Full-Size Img PowerPoint

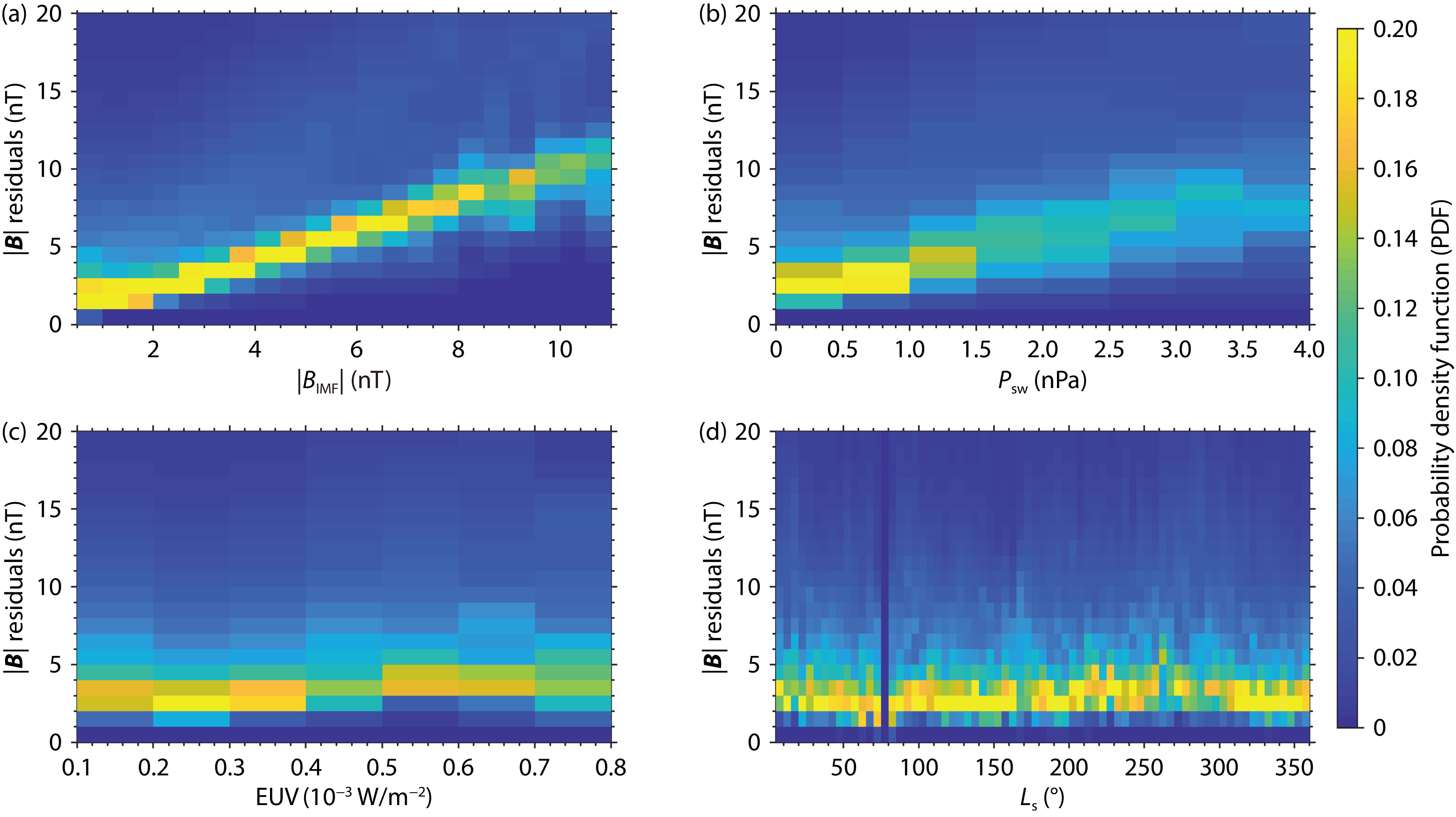
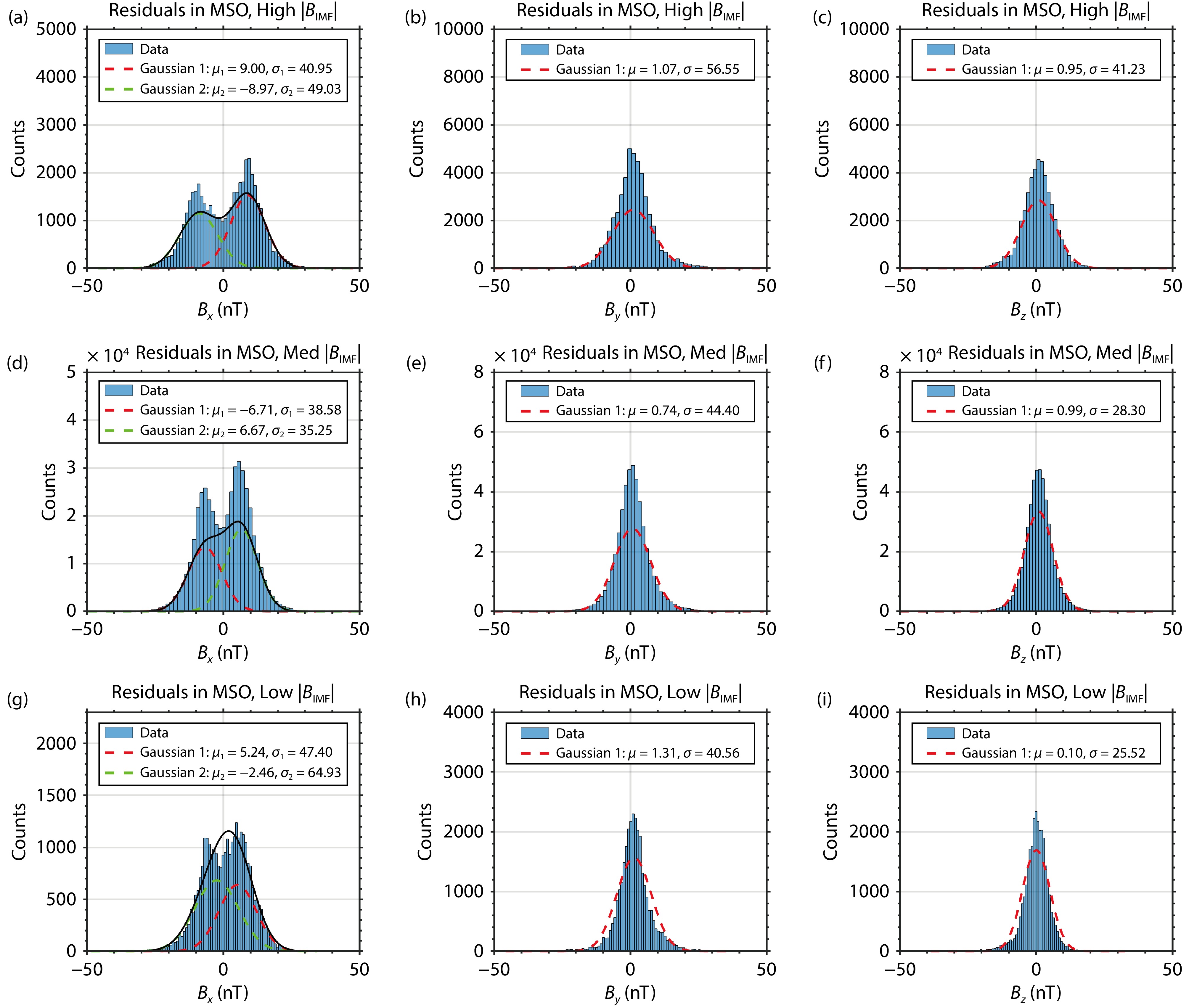
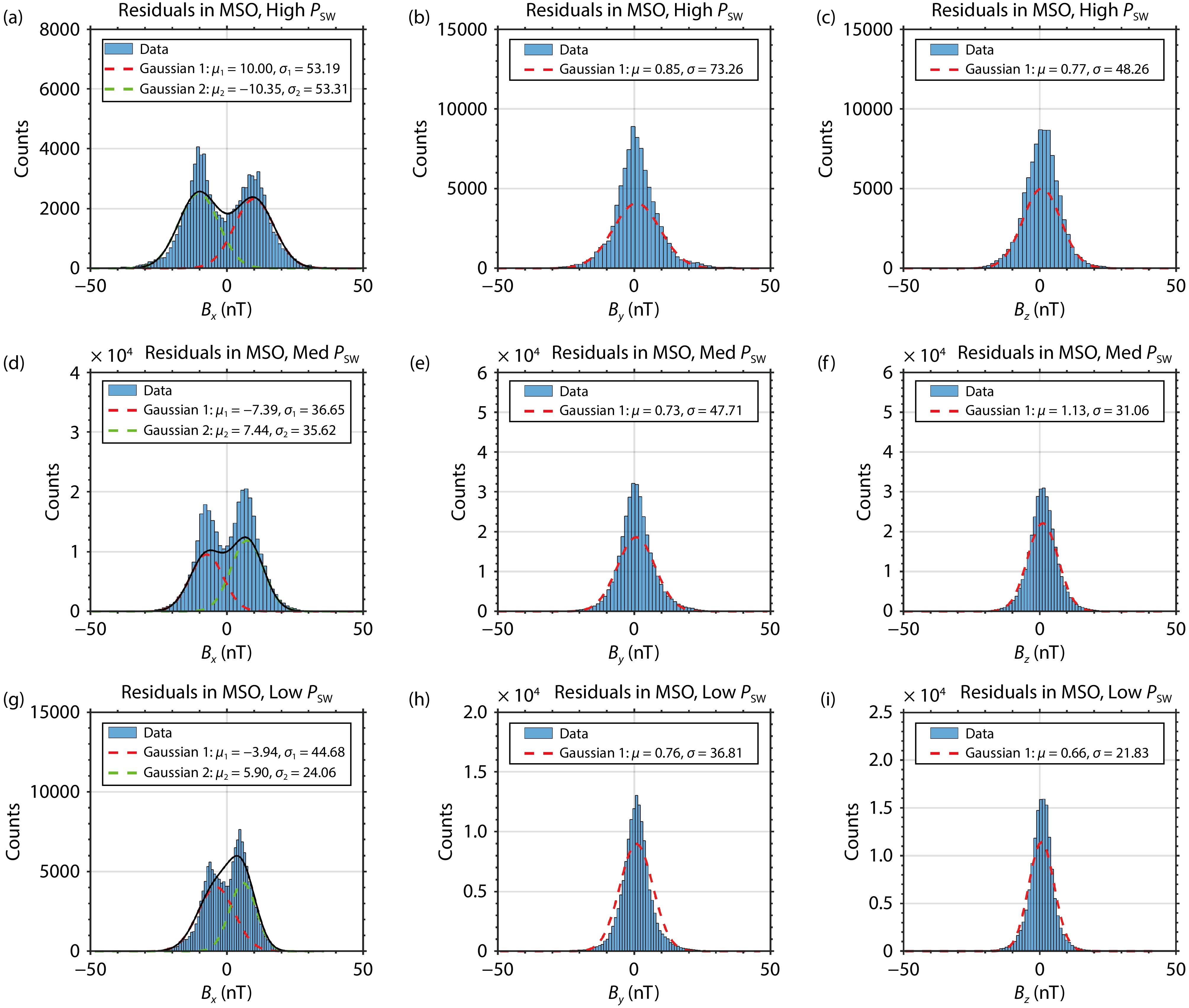
Figure 3 illustrates conditional probability density functions of magnetic field residuals in the nightside ionosphere, as influenced by the upstream drivers. Previous research has identified positive correlation between the $\left|{\boldsymbol{B}}_{{\mathrm{IMF}}}\right|$ and magnetic field residuals, suggesting increased residuals during periods of high $\left|{\boldsymbol{B}}_{{\mathrm{IMF}}}\right|$ (Mittelholz et al., 2018). Figure 4a and b show that we, too, find not only that $\left|{\boldsymbol{B}}_{{\mathrm{IMF}}}\right|$ exhibits positive correlation with the residuals, but so does ${P}_{{\mathrm{SW}}}$. We also find less pronounced correlations between magnetic field residuals and both EUV and ${L}_{{\mathrm{s}}}$, noting, however, that residuals may increase during periods of high solar irradiance, and when Mars is near its perihelion (${L}_{{\mathrm{s}}}$ = 250−300).

Figure  4.  Conditional probability density functions of Martian nightside magnetic field residuals as a function of these upstream drivers: (a) intensity of IMF ($\left|{\boldsymbol{B}}_{{\mathrm{IMF}}}\right|$), (b) solar wind dynamic pressure (${P}_{{\mathrm{SW}}}$), (c) EUV flux, and (d) Martian season (L_s). The probability density functions are normalized for each driver within each bin.

DownLoad: Full-Size Img PowerPoint

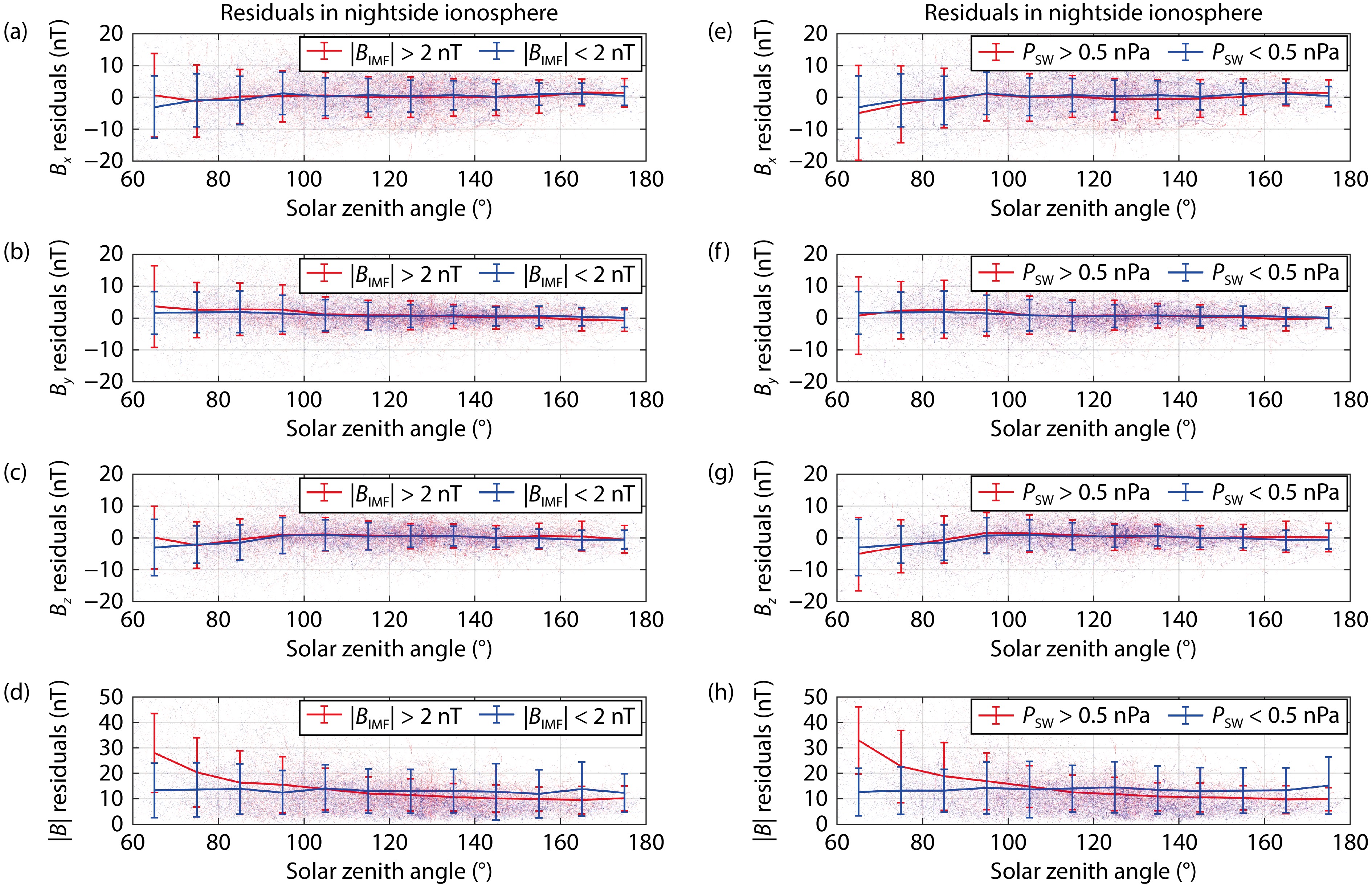
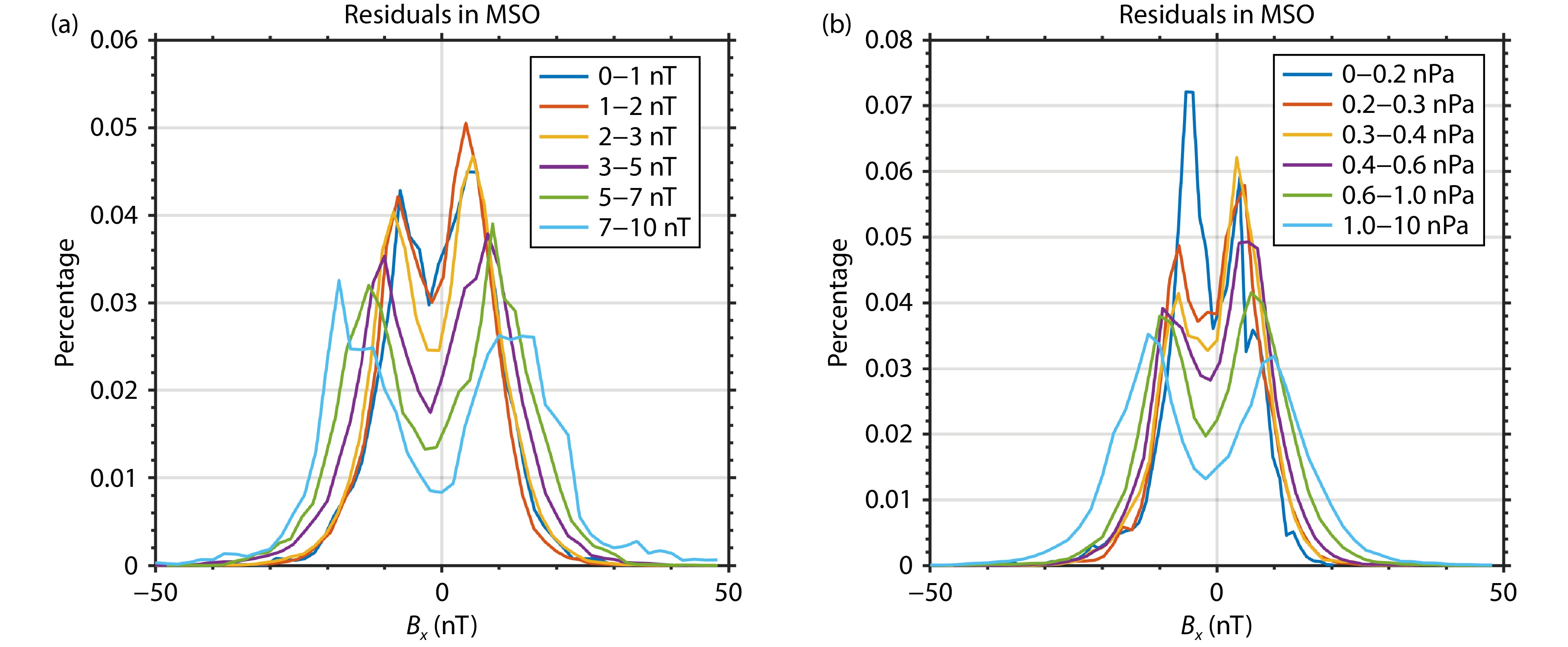
Figure 5 illustrates the variation of ionospheric magnetic field residuals, measured below 600 km altitude, with the solar zenith angle (SZA) under conditions of low and high $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$, respectively. The standard deviation of the residuals within each SZA bin (10°) is represented by error bars, which are centered on the average strength of the external magnetic field. The two categories of $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ are defined as $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ < 2 nT and $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ > 2 nT , and ${P}_{\rm{SW}}$ < 0.5 nPa and ${P}_{\rm{SW}}$ > 0.5 nPa, considering that the median values of upstream $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ are 2 nT and 0.5 nPa, respectively. Previous research has suggested that the dependence of ionospheric magnetic field residuals on the solar zenith angle is governed by both $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ (e.g., Luhmann and Cravens, 1991; Byrd et al., 2024). We observe that the residuals decrease with SZA on the nightside. During conditions of high $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$, the residuals are indeed stronger on the nightside (SZA = 120°−160°) for the ${B}_{x}$ component, while the ${B}_{y}$ and ${B}_{z}$ components do not exhibit any significant increase. Furthermore, we note a significant increase in dayside residuals during high $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ conditions, from ~20 nT to ~50 nT. This increase is likely due to stronger ionospheric currents, which are induced to counterbalance the heightened solar wind dynamic pressure. These currents subsequently lead to a more significant ionospheric magnetic field. We also observe higher $\left|{\boldsymbol{B}}\right|$ residuals around midnight (SZA = 140°−180°) under low $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ conditions, which may be attributable to tighter wrapping of the IMF on the nightside under those conditions.

Figure  5.  Variation of the ionospheric external magnetic field with solar zenith angle (SZA) for (a−d) $\left|{\boldsymbol{B}}_{{\mathrm{IMF}}}\right|$ and (e−h) ${P}_{{\mathrm{SW}}}$. Panels from top to bottom show the scatter maps of the external magnetic field ${B}_{x}$, ${B}_{y}$, ${B}_{z}$ and $\left|{\boldsymbol{B}}\right|$ in MSO coordinates. Error bars indicate the standard deviation of the average magnetic field within each solar zenith angle bin (10° in SZA). The red and blue error bars represent the standard deviation of the magnetic field for high and low $\left|{\boldsymbol{B}}_{{\mathrm{IMF}}}\right|$ and ${P}_{{\mathrm{SW}}}$ conditions, respectively.

DownLoad: Full-Size Img PowerPoint

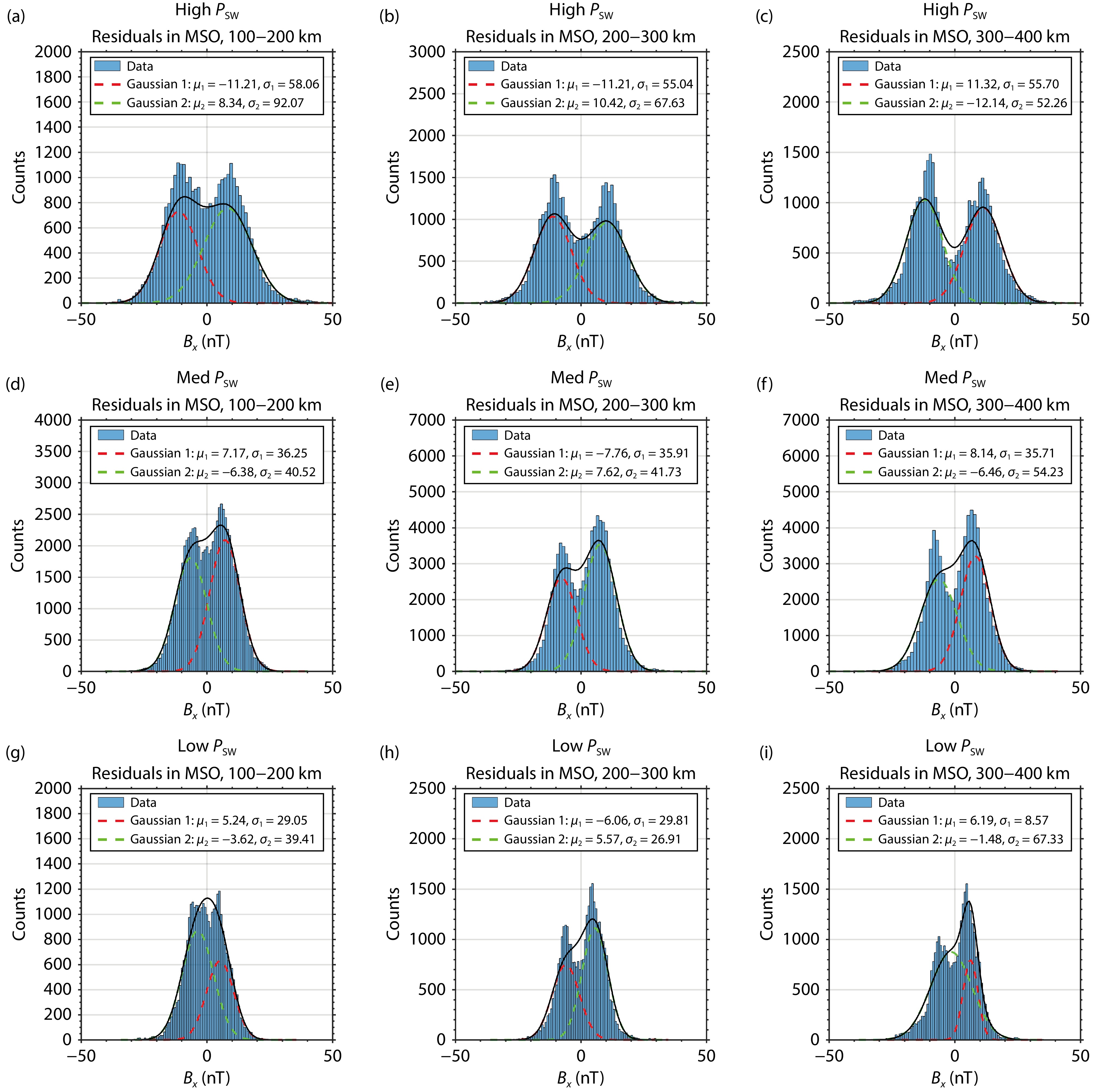
Figure 6 and Figure 7 show histograms of nightside magnetic field residuals — ${B}_{x}$, ${B}_{y}$, and ${B}_{z}$ components — under various upstream conditions. The distribution of the ${B}_{x}$ component is similar to a bi-modal normal distribution, a superposition of two normal distributions, while the distributions for the ${B}_{y}$ and ${B}_{z}$ components are similar to a normal distribution. This suggests that the residuals are mainly contributed to by the draped IMF, which consists of two magnetic field lobes in the nightside ionosphere (Ferguson et al., 2005). The bi-modal nature of the ${B}_{x}$ component corresponds closely to the observed warping and draping patterns of the IMF, whereas the distributions of the ${B}_{y}$ and ${B}_{z}$ components are consistent with the ionosphere looping field. However, the magnetic field topology in the Martian ionosphere has not been definitively established; thus, detailed discussions of the magnetic field topology are not included in this study.

Figure  6.  Histograms of the nightside magnetic field residuals in the non-crustal field regions under upstream high $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ (a−c), medium $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ (d−f), and low $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ (g−i) conditions. Panels from left to right show the magnetic field ${B}_{x}$, ${B}_{y}$, and ${B}_{z}$ components. The red and green curves represent the distribution functions fitted to the histogram, with the ${B}_{x}$ component being fitted with a bi-modal normal distribution and the ${B}_{y}$ and ${B}_{z}$ components being fitted with a normal distribution. The means ($\mu$) and standard deviations ($\sigma$) of the normal distributions are detailed in the legend. The condition for ${P}_{\rm{SW}}$ is selected as medium.

DownLoad: Full-Size Img PowerPoint

Figure  7.  Histograms of the nightside magnetic field residuals in the non-crustal field regions under upstream high ${P}_{\rm{SW}}$ (a−c), medium ${P}_{\rm{SW}}$ (d−f), and low ${P}_{\rm{SW}}$ (g−i) conditions. The format is the same as that of Figure 6. The condition for $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ is selected as medium.

DownLoad: Full-Size Img PowerPoint

For reasons stated above, we chose a bi-modal normal distribution to fit the probability density function of the ${B}_{x}$ component, but have fitted the ${B}_{y}$ and ${B}_{z}$ components using a normal distribution, with means and standard deviations denoted by $\mu$ and $\sigma$, respectively (Lloyd, 1982). The bi-modal normal distribution was fitted using a Gaussian mixture model via the Expectation-Maximization (EM) algorithm. Initial values for the Gaussian mixture model parameters were selected using the k-means algorithm (McLachlan et al., 2019). This approach has allowed us to estimate the separation of the bi-modal normal distribution quantitatively by the distribution’s two mean values (${\mu }_{1}$ and ${\mu }_{2}$). The ${B}_{x}$ component’s mean values reached approximately 10 nT under high $|{\boldsymbol{B}}_{\rm{IMF}}|$ and ${P}_{\rm{SW}}$, but were approximately 5 nT under low $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$, suggesting that the strength of the draped IMF in the nightside ionosphere is larger under high $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ conditions. Furthermore, under high $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$, the standard deviations ($\sigma$), which describe the dispersion of data around their means, for all three magnetic field components are relatively larger, increasing from ~40 under low $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ to ~60 under high $|{\boldsymbol{B}}_{\rm{IMF}}|$ and ${P}_{\rm{SW}}$.

Figure 8 shows the variance in the distribution of the ${B}_{x}$ component’s magnetic field residuals, according to varying upstream $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ conditions. We observe that across a range of upstream $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ conditions, from the lowest to the highest, the distribution of the ${B}_{x}$ component is consistently bi-modal. It becomes evident that the separation between the two peaks in the ${B}_{x}$ distribution widens as $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ increase. When the strengths of upstream $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ reach particularly high levels, specifically between 7−10 nT for $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and 1−10 nPa for ${P}_{\rm{SW}}$, the mean values of the ${B}_{x}$ component are approximately 11−14 nT. In contrast, under moderate and low upstream $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ conditions, these values are about 5−8 nT.

Figure  8.  Histograms of the nightside magnetic field residuals in the non-crustal field regions under various upstream (a) $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$, and (b) ${P}_{\rm{SW}}$ conditions. Solid lines indicate the distributions of magnetic field residuals, organized by the intensity of $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$. To encompass the spectrum of upstream variations, six groups were delineated for both $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ conditions.

DownLoad: Full-Size Img PowerPoint

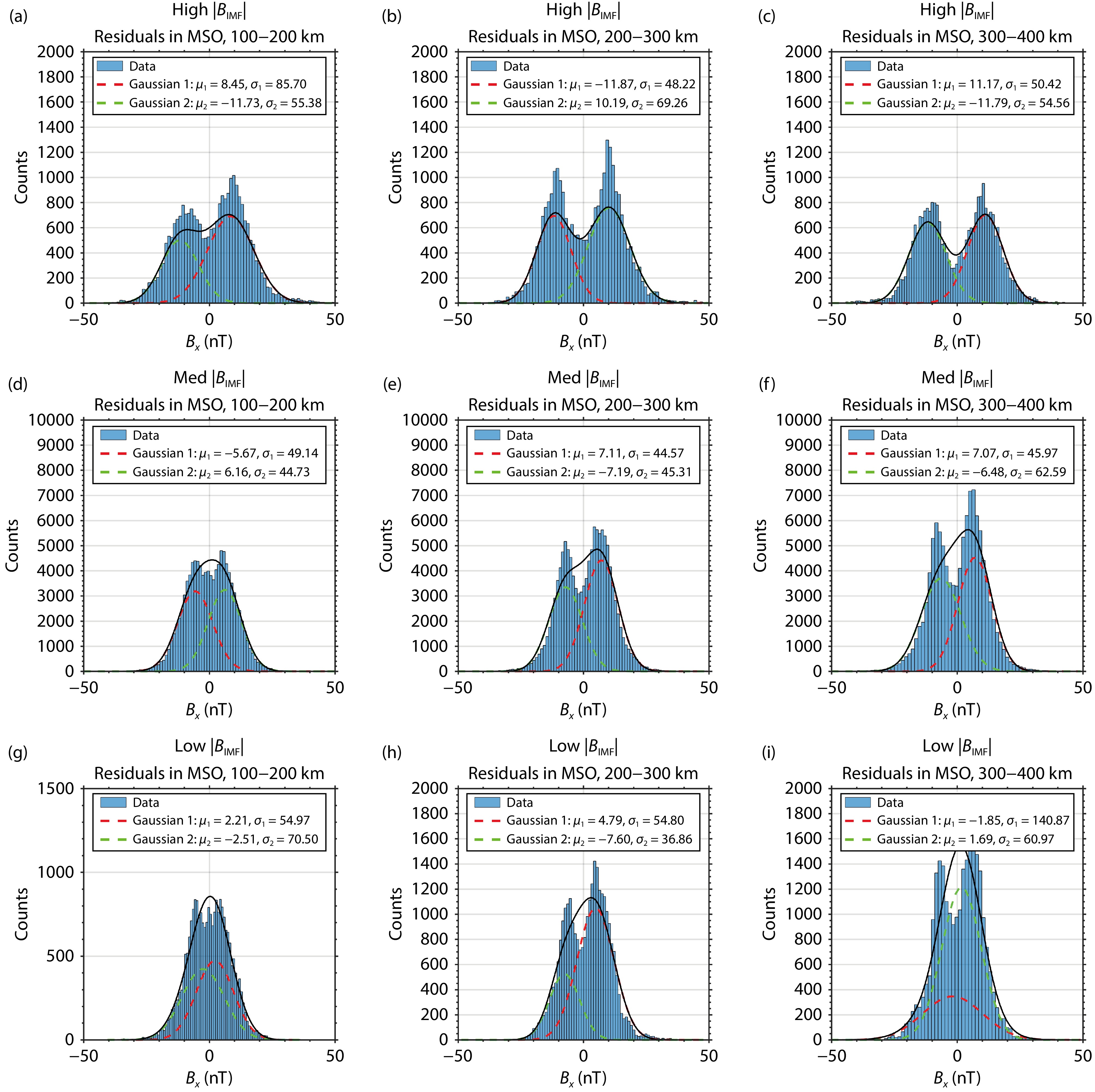
Previous studies have shown that the IMF can extend as far inward as the MGS mapping altitudes, reaching up to 400 km (Brain et al., 2020). The bi-modal distribution of the ${B}_{x}$ component serves as a useful indicator of the altitude at which IMF draping occurs. In this study, we analyzed the distribution of the ${B}_{x}$ component across altitude ranges of 100−200 km, 200−300 km, and 300−400 km under various upstream $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ conditions, as shown in Figure 9 and Figure 10. Our findings suggest that the draping IMF can penetrate to altitudes of 200−300 km, regardless of the upstream $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ conditions. At an altitude range of 200−400 km, under conditions of high $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$, the strength of the IMF can reach approximately 10 nT, whereas this value decreases to about 5 nT under low $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ conditions. At the 100−200 km altitude range, when the upstream $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ conditions are high to medium, the ${B}_{x}$ component exhibits a clear bi-modal distribution. However, under low $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ conditions, the ${B}_{x}$ component is similar to a normal distribution. This indicates that the IMF penetrates weakly, if at all, to the 100−200 km altitude range when $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ conditions are low.

Figure  9.  Histograms of nightside magnetic field residuals across three altitude ranges under upstream high $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ (a−c), medium $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ (d−f), and low $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ (g−i) conditions. Panels from left to right show the magnetic field distribution within altitude ranges of 100−200 km, 200−300 km, and 300−400 km, respectively.

DownLoad: Full-Size Img PowerPoint

Figure  10.  Histograms of nightside magnetic field residuals across three altitude ranges under upstream high ${P}_{\rm{SW}}$ (a−c), medium ${P}_{\rm{SW}}$ (d−f), and low ${P}_{\rm{SW}}$ (g−i) conditions. Panels from left to right show the magnetic field distribution within altitude ranges of 100−200 km, 200−300 km, and 300−400 km, respectively.

DownLoad: Full-Size Img PowerPoint

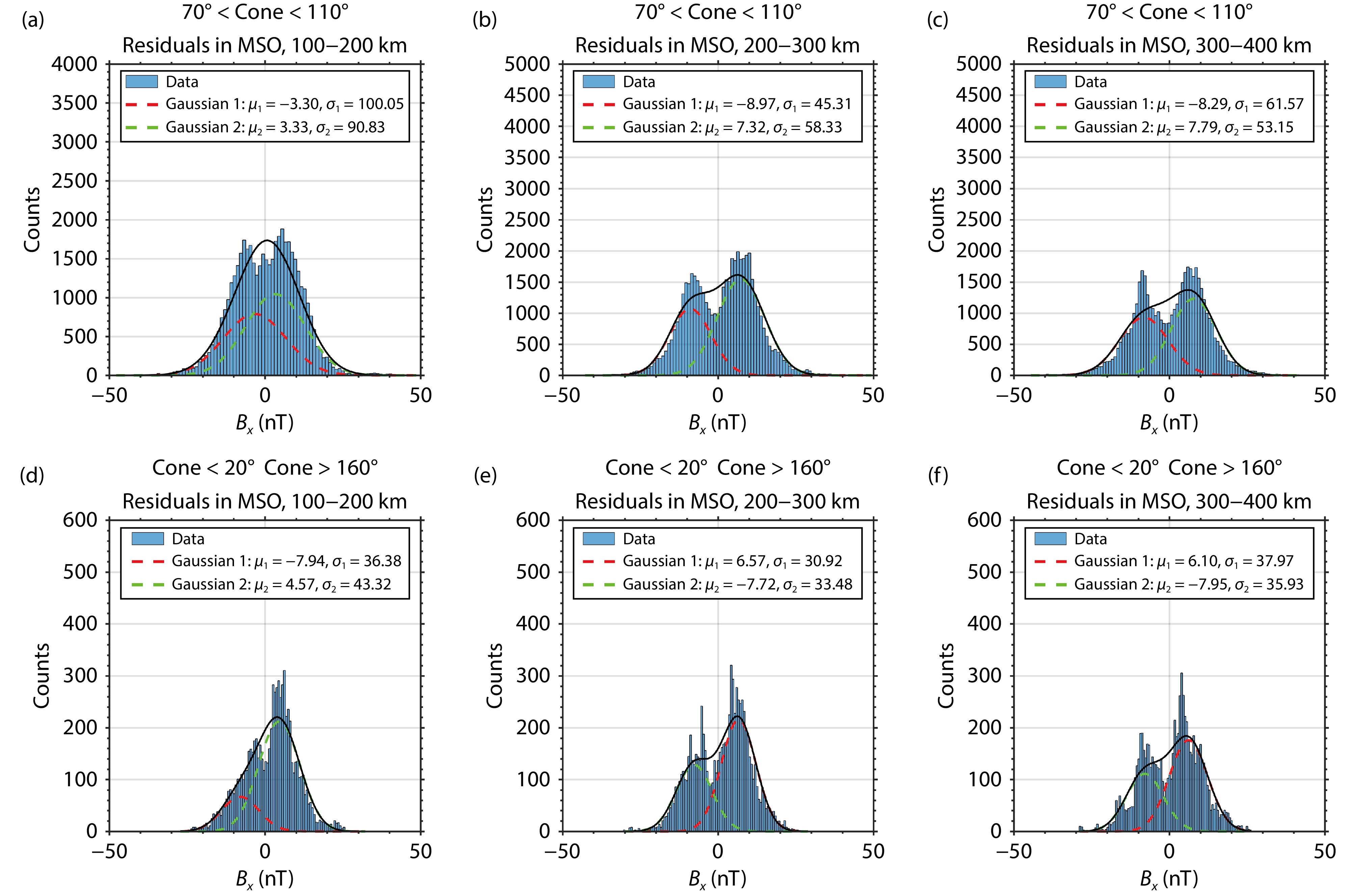
The IMF penetrating altitude may also depend on the solar EUV radiation and the IMF cone angle. Brain et al. (2020) suggested that during periods of high EUV, an increase in photoionization leads to heightened ionospheric thermal pressure on the dayside and near the terminator, thereby inhibiting the penetration of a draped IMF into the ionosphere. Moreover, the influence of the IMF direction, particularly the cone angle, on the topology of the magnetic field in the Martian magnetosphere has been well recognized (e.g., Burne et al., 2021; Zhang C et al., 2022; Zhang Q et al., 2023). However, the effect of the IMF cone angle on the penetrating altitude of the IMF has not been thoroughly explored. Figure 11 and Figure 12 illustrate histograms of nightside magnetic field residuals across three altitude ranges under varying EUV flux and IMF cone angle conditions. In this study, we define the IMF cone angle as the angle between the projected IMF and ${+X}_{\rm{MSO}}$ direction in the ${XY}_{\rm{MSO}}$ plane, rotating from ${+X}_{\rm{MSO}}$ toward ${+Y}_{\rm{MSO}}$ (See Figure 2 in Liu D et al., 2021). Accordingly, our dataset is categorized into two subsets: the quasi-perpendicular IMF (cone angle 70°−110°) and the quasi-parallel IMF (cone angle <20° or >160°) conditions.

Figure  11.  Histograms of nightside magnetic field residuals across three altitude ranges under upstream high EUV (a−c) and low EUV (d−f) conditions. Panels from left to right show the magnetic field distribution within altitude ranges of 100−200 km, 200−300 km, and 300−400 km, respectively. The condition for $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ are selected as medium.

DownLoad: Full-Size Img PowerPoint

Figure  12.  Histograms of nightside magnetic field residuals across three altitude ranges under upstream conditions with cone angle 70°−110° (a−c) and cone angle <20° or >160° (d−f). Panels from left to right show the magnetic field distribution within altitude ranges of 100−200 km, 200−300 km, and 300−400 km, respectively. The condition for $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ are selected as medium.

DownLoad: Full-Size Img PowerPoint

Figure 11 demonstrates that under both high and low EUV conditions, the IMF can penetrate to an altitude of 200−300 km. Below 200 km altitude, the separation between the two peaks in the ${B}_{x}$ distribution becomes wider under high EUV conditions. Figure 12 reveals that under both quasi-parallel and quasi-perpendicular IMF conditions, the IMF can penetrate to altitudes lower than 200 km. Additionally, we observed that the standard deviations of the magnetic field residual distributions are higher under quasi-perpendicular IMF conditions than under quasi-parallel conditions.

4.   Discussion and Conclusion

Using MAVEN data from November 2014 to May 2023, we have investigated the distribution of magnetic field residuals in the Martian nightside ionosphere under four upstream solar wind drivers: the intensity of the IMF ($\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$), solar wind dynamic pressure (${P}_{\rm{SW}}$), solar extreme ultraviolet (EUV) flux, and Martian seasons (${L}_{\rm{s}}$). Our key findings are summarized below:

(1) The magnetic field residuals in the Martian ionosphere show significant positive correlation with $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$; they are weakly correlated with EUV flux and ${L}_{\rm{s}}$. The residuals are notably higher during periods of high EUV flux, and when Mars is near its perihelion (${L}_{\rm{s}}$ = 250°−300°).

(2) Under varying upstream conditions, including both high and low $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ and EUV conditions, the IMF can penetrate to an altitude of 200 km in the nightside ionosphere. Specifically, the IMF can reach the 100−200 km altitude range under high and medium $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ conditions, namely, $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ > 1 nT and ${P}_{\rm{SW}}$ > 0.3 nPa.

(3) The distribution of upstream EUV and IMF cone angles does not significantly affect the altitude to which the IMF penetrates. However, we observe that the separation of the bi-modal normal distribution of the ${B}_{x}$ component is larger under high EUV conditions, and the standard deviations of the residual’s distributions are higher under quasi-perpendicular IMF conditions.

In the Martian ionosphere, the external magnetic field originates from two primary sources. The first is the interaction between the solar wind and the ionosphere, resulting in the draping and stacking of the IMF at ionospheric altitudes (e.g., Ferguson et al., 2005; Fang XH et al., 2023). The second source is the ionospheric magnetic field generated by ionospheric currents powered by the ionospheric dynamo (e.g., Mittelholz et al., 2017; Lillis et al., 2019). These two sources of the external magnetic field can be distinguished in Figure 5. The ionospheric magnetic field generated by ionospheric currents reaches its maximum intensity at dayside, while in the nightside ionosphere it is the draped IMF that dominates the ${B}_{x}$ component, exhibiting a bi-modal distribution (Figure 6a); the nightside ionospheric magnetic field itself exhibits a normal distribution (Figure 6b and c).

The observed positive correlation between $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ with magnetic field residuals is readily understandable (Crider et al., 2003). Typically, both $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ are higher during solar extreme dynamic pressure events, such as coronal mass ejections (CMEs) and co-rotating interaction regions (CIRs). An increase in $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ leads to a higher intensity of the draped IMF, and a rise in ${P}_{\rm{SW}}$ suggests that the IMF can penetrate to lower altitudes. Consequently, we observe larger magnetic field residuals under conditions of high $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$. Moreover, the residuals tend to increase under conditions of high EUV flux and when Mars is near its perihelion. We propose two potential explanations for this observation: First, the EUV flux is notably higher at Mars’ perihelion, the point of smallest Sun−Mars distance, coinciding with a period of relatively higher solar wind dynamic pressure (Girazian et al., 2023). Therefore, the increase in residuals during periods of high EUV flux may result from the higher solar wind dynamic pressure experienced at Mars’ perihelion. Second, around Mars’ perihelion, specifically at ${L}_{\rm{s}}$ = 250°−300°, Mars encounters its global dust storm season (Montabone et al., 2015). The combination of high EUV flux and global dust storms is likely to enhance atmospheric circulation, possibly resulting in a more intense ionospheric dynamo. As a consequence, the intensity of the external magnetic field, generated by ionospheric currents, would see an increase. This hypothesis will be further examined as our understanding of the impact of dust storms on the external magnetic field advances (Mittelholz et al., 2020).

Figure 9 and Figure 10 indicate that the altitude at which the IMF penetrates the Martian nightside ionosphere varies in response to multiple external factors. The IMF can reach an altitude of 100−200 km under high and medium $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$, while it can extend to 200−300 km under low $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$. Contrary to the ionosphere of Venus, which can be distinctly categorized into magnetized and unmagnetized states (Byrd et al., 2024), the Martian nightside ionosphere appears to be magnetized most of the time, given that the IMF can penetrate to altitudes of approximately 100−200 km. Moreover, the influence of EUV flux and IMF cone angle on the altitude of IMF penetration is not significant, despite EUV radiation being a primary driver of the Martian ionosphere above ~100 km (e.g., Withers et al., 2019; Sánchez-Cano et al., 2020). EUV radiation does not induce significant perturbations to the external magnetic field, compared to other factors such as $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$. This might be due to solar EUV reaching its peak photoionization effects at altitudes lower by approximately 40 km than the peak of the external magnetic field (Fang XH et al., 2023). Additionally, the distribution of nightside magnetic field residuals does not significantly change under both quasi-parallel and quasi-perpendicular IMF conditions. This suggests that the process of IMF piling up is not sensitive to the direction of the IMF, and the magnetotail-like feature in the nightside ionosphere of Mars shows no significant dependence on the flow-aligned component of the IMF (Rong ZJ et al., 2016).

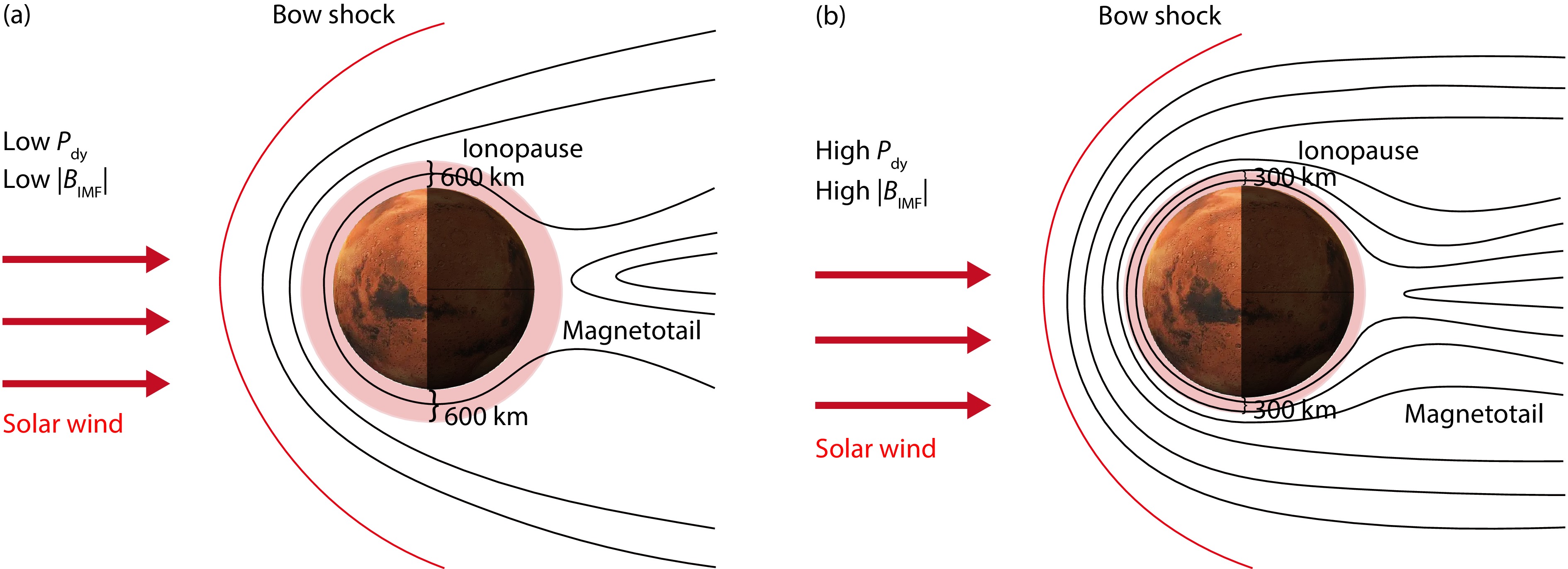
Our findings in this study are summarized in Figure 13, which illustrates the configuration of the magnetic field around Mars under varied $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ conditions. Generally, the observed magnetic field wraps around the dayside of Marian ionosphere and continues to conform to the planet’s shape on the nightside, reversing its direction to form a nearly complete torus. At ionospheric altitudes, the intensity of the draped IMF decreases with increasing SZA, as noted by Luhmann and Cravens (1991). Contrasting with the diagrams from earlier studies, such as Figure 9 in Luhmann et al. (1981), our research quantitatively determines the altitude at which the IMF penetrates the nightside of Mars. The draped IMF in the Martian nightside ionosphere could lead to the acceleration of plasma. Under varying upstream conditions, the IMF can penetrate to approximately 200 km altitude, forming localized channels for planetary ion escape (Shuvalov et al., 2024). In the past, the solar wind exhibited higher $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ than are observed in today’s solar wind (e.g., Kulikov et al., 2007). On ancient Mars, the IMF could have penetrated much deeper than today’s draping altitude, potentially resulting in a much higher escape rate for ancient Mars compared to today. We anticipate that measurements of plasma velocities at low altitudes in the Martian ionosphere will confirm this hypothesis. Our next study will aim to determine whether these loss rates could have had a significant atmospheric escape impact when considered over the age of the solar system.

Figure  13.  Illustration of the magnetic field configuration in the meridian plane under high $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ conditions (a) and under low $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ conditions (b). The tail current sheet is oriented perpendicular to the meridian plane. The red line indicates the position of the bow shock. Note that the shape of bow-shock is larger during low $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ and ${P}_{\rm{SW}}$ (Garnier et al., 2022).

DownLoad: Full-Size Img PowerPoint

Lastly, regarding the modeling of the internal magnetic field, we establish a selection criterion indicating that the magnetic condition is ‘quiet’, signifying that the external magnetic field is relatively weak and, consequently, the magnetic field residuals are relatively smaller. Previous studies have demonstrated that $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ serves as a useful magnetic field activity index (Mittelholz et al., 2018). Based on Figure 3, we suggest that the magnetic ‘quiet’ condition should be satisfied when $\left|{\boldsymbol{B}}_{\rm{IMF}}\right|$ < 2 nT, ${P}_{\rm{SW}}$ < 1 nPa, EUV < $0.5\times {10}^{-3}$ ${{\mathrm{W/m}}}^{2}$, and data near the Mars perihelion (${L}_{\rm{s}}$ < 250° or ${L}_{\rm{s}}$ > 300°) are disregarded.