Mshpy23: a user-friendly, parameterized model of magnetosheath conditions

1.   Introduction

Magnetic reconnection is a key process that transfers mass, momentum, and energy from solar wind to the Earth’s magnetosphere. Recent series of satellites, namely Cluster, Time History of Events and Macroscale Interactions during Substorms (THEMIS), and Magnetospheric Multiscale (MMS), have enabled a space science community to study smaller and smaller scales of magnetic reconnection, greatly improving our understanding of fundamental physics. However, these in-situ measurements are somewhat limited for studying global-scale reconnection that governs the holistic behavior of the Earth’s magnetospheric systems under the dynamic solar wind and interplanetary magnetic field (IMF) conditions.

Recently, Lunar Environment heliospheric X-ray Imager (LEXI; http:sites.bu.edu/lexi) and Solar wind−Magnetosphere−Ionosphere Link Explorer (SMILE; Branduardi-Raymont et al., 2018) are scheduled to launch in 2024 and 2025, respectively, for addressing global nature of the solar wind−magnetosphere interaction. Both LEXI and SMILE will have a wide field-of-view soft X-ray imager on board, observing the soft X-rays emitted in the magnetosheath by the charge exchange between highly charged solar wind ions and exospheric hydrogen atoms. The soft X-ray images can capture the magnetosheath and its boundary motion under dynamic solar wind/IMF conditions, helping to understand the large-scale reconnection pattern on the magnetopause. LEXI will provide wide field-of-view images of the Earth’s dayside system from the lunar surface during its operation period of less than 2 weeks. SMILE will also observe the dayside system in soft X-ray but from a highly-elliptical polar orbit, providing over 40 hours of continuous images per orbit during its 3-year mission period.

Magnetosheath plasma number density, velocity, and temperatures are required parameters for calculating a soft X-ray image of the Earth’s dayside system. Previous studies (Connor et al., 2021, Sun TR et al., 2019) utilized global magnetohydrodynamics (MHD) models to create expected soft X-ray images from various vantage points. Although MHD models (Raeder et al., 2001; Tóth et al., 2005; Lu JY et al., 2019a; Qu BH et al., 2021) provides realistic magnetosheath parameters during various solar wind/IMF conditions, the simulation takes considerable time, and the analysis of the modeling results requires sophisticated techniques and knowledge of a particular model in use, which may be a difficult task for non-experts of modeling.

This paper developed a user-friendly magnetosheath model that parameterizes plasma and magnetic field conditions based on MHD, gas-dynamic, and analytic models. First, we developed an MHD-based magnetosheath model and compared its results with THEMIS data of 2007–2014. Second, by adding several magnetosheath models in the previous literature, we compiled a suite of magnetosheath models, Mshpy23. We compared the result of each model in the Mshpy23 suite with the in-situ data of Cluster and THEMIS. Finally, we showed an example of X-ray image simulation using our MHD-based magnetosheath model. Our Mshpy23 code is written in Python3 and publicly available at https://github.com/jjung11/Mshpy.

2.   MHD-Based Magnetosheath Model

2.1   Coordinates and Boundaries

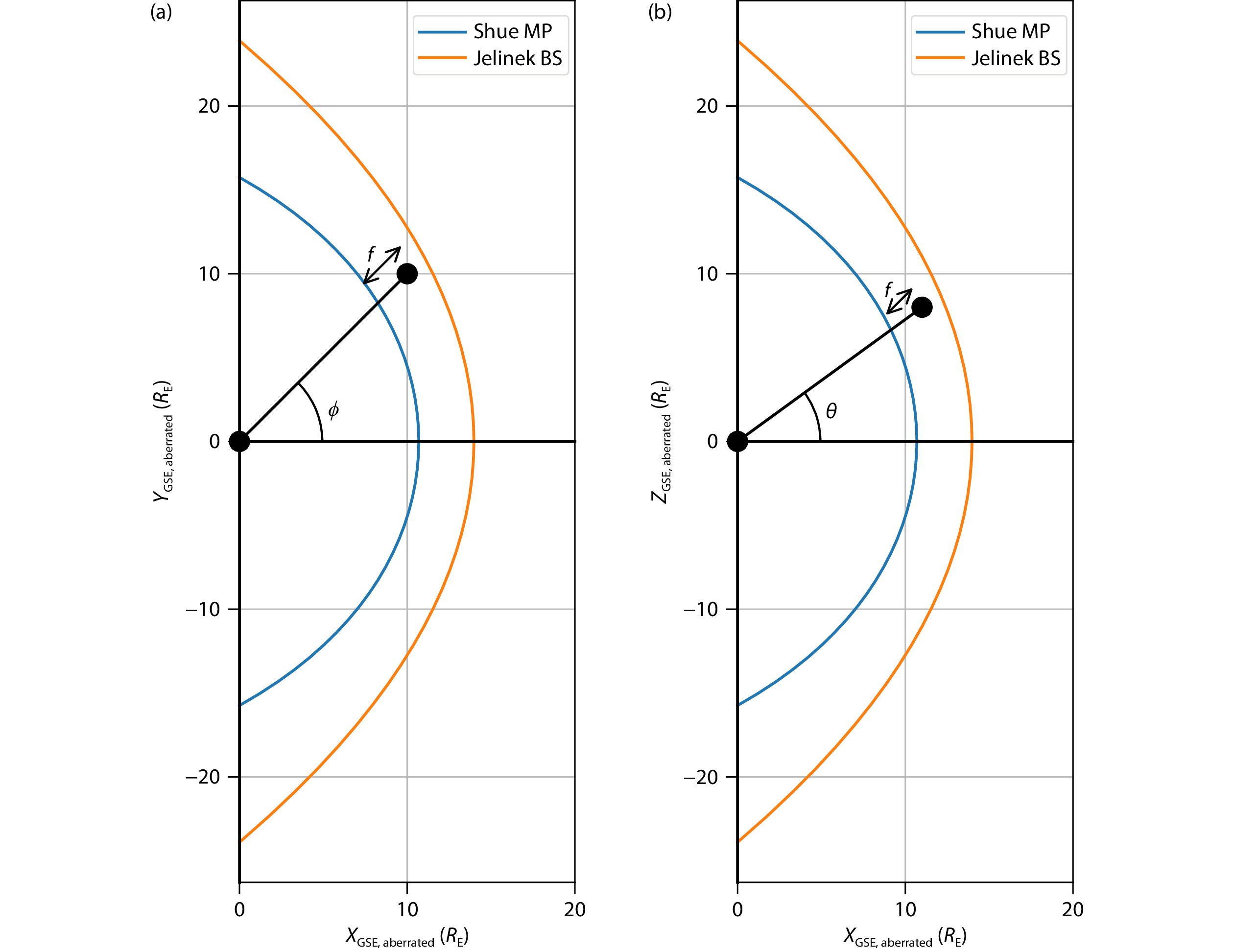
One of the most commonly used coordinate systems in space physics is Geocentric Solar Ecliptic (GSE) coordinates system. It has its X-axis pointing from the Earth’s center toward the Sun and Z-axis pointing in the direction of the north ecliptic pole. The Y-axis lies on the ecliptic plane, pointing an opposite direction to the Earth’s orbit around the Sun. However, the GSE coordinate system is not ideal for the magnetosheath parameter model because the bow shock (BS) and magnetopause (MP) continuously move in response to solar wind/IMF conditions. Instead, we adopted a new coordinate system for our magnetosheath model. First, we converted GSE to aberrated GSE coordinates, to account for the Earth’s orbital motion. In that way, the incoming, upstream solar wind is parallel to the X-axis. Next, we adopted two angles and a fractional distance to represent a point in the magnetosheath, as seen in Figure 1. Two angles are longitude ($\phi$) and latitude ($\theta$) in aberrated GSE coordinates and the fractional distance (f) is

Figure  1.  Diagram of the magnetosheath model coordinates. (a) longitude $\phi$ in the XY plane and (b) latitude $\theta$ in the XZ plane with a fractional distance $f$ between MP ($f$ = 0; blue curve) and BS ($f$ = 1; orange curve). The aberrated GSE coordinates are used in these plots.

DownLoad: Full-Size Img PowerPoint

where $\boldsymbol{R}$ is the aberrated GSE position vector and $r_{{\mathrm{mp}}}$ and $r_{{\mathrm{bs}}}$ are the geocentric distance to the MP/BS in the given latitude and longitude direction, respectively. In our magnetosheath coordinates, f = 0 indicates the MP location and f = 1 the BS location.

This new magnetosheath coordinate system requires magnetosheath boundary locations. Numerous empirical models of the MP have been developed in the literature, primarily based on satellite crossing observatoins. Key references in this field include works by Fairfield (1971), Sibeck et al. (1991), Roelof and Sibeck (1993), Petrinec and Russell (1993, 1996), Kuznetsov and Suvorova (1998), Shue et al. (1997, 1998), Boardsen et al. (2000), Chao JK et al. (2002), Lin RL et al. (2010), Lu JY et al. (2011), and Liu ZQ et al. (2015). These models often utilize ellipsoidal or quadratic equations or adopt the Shue model function to describe the MP. They parameterize MP crossings at low latitudes, taking into account factors like solar wind dynamic pressure and the IMF $B_z$ component. Notably, Shue 1998 model has gained widespread recognition for its versatility in predicting both open and closed MP configurations along with its ability to provide reasonable predictions for the distant tail region. Recent developments have led to models accounting for MP shape asymmetry, including those proposed by Lin RL et al. (2010); Lu JY et al. (2011); and Liu ZQ et al. (2015).

Regarding Earth’s BS, a multitude models has been proposed since its prediction and discovery, starting with Seiff (1962) and Spreiter et al. (1966). These models aim to replicate the BS’s standoff distance, shape, and responses to solar wind parameter variations. many of these models are based on the fitting of observed BS crossing while incorporating gas-dynamic or MHD principles, as demonstrated by Němeček and Šafránková (1991) and Peredo et al. (1995). In contrast, some models rely on MHD simulations results, as exemplified by Cairns and Lyon (1995). Jeřáb et al. (2005) improved the 3-D empirical BS model initially proposed by Němeček and Šafránková (1991) through modifications to the BS surface function. Merka et al. (2005) introduced corrections to the Peredo et al. (1995) model, focusing on the effects of upstream Mach number on the BS. Following the case of MP modeling, there have been efforts to model BS asymmetry recently (Wang M et al., 2018; Lu JY et al., 2019b).

Currently we have implemented a magnetopause model of Shue et al. (1998) and a bow shock model of Jelínek et al. (2012), due to their simple model formulation and wide usage. Shue et al. (1998) developed a widely-used, empirical MP model with boundary crossing data of ISSEE1/2, AMPTE/IRM, IMP8, and, Interball 1 satellites. Based on the model, the radial distance of the MP is given by:

where $\theta_z$ is the solar zenith angle, and the standoff distance $r_0$ and the level of tail flaring $\alpha_1$ are given by:

The parameters $r_0$ and $\alpha_1$ depend on IMF $B_z$ and solar wind dynamic pressure $P_d$.

Jelínek et al. (2012) developed an empirical BS model by using the THEMIS data and a method of determination of the most propable boundary locations. The following equation explains the BS shape as a function of aberrated GSE coordinates.

where $R_0$ = 15.02 $R_{{{\mathrm{E}}}}$, $\lambda$ = 1.17, $\epsilon$ = 6.55, and $P_d$ is the solar wind dynamic pressure. We also included a BS model of Jeřáb et al. (2005) in Mshpy23. Jeřáb et al. (2005) utilized only BS crossing data below $X _{{{{\mathrm{GSE}}}}}$ < 8 $R_{\mathrm{E}}$ (flank region) and thus their model tends to locate the BS more earthward than the Jelínek’s BS model, creating a very narrow magnetosheath (< 1 $R_{\mathrm{E}}$) under most solar wind/IMF conditions when combined with the MP model of Shue et al. (1998). To avoid this issue, we adopted the BS model of Jelínek et al. (2012) as a default BS model of Mshpy23, while providing an option for users to manually select their preferred BS model.

Our MHD-based model, also named Mshpy23-MHD, operates like the following. First, a user inputs a location of interest in a typical GSE coordinate system along with solar wind and IMF conditions at the bow shock nose. Then, our model calculates magnetosheath boundaries under the given solar wind conditions and obtains f, $\theta$, and $\phi$ of the input location by using the boundary information. Finally, the model calculates magnetosheath parameters at the given point by linearly interpolating the MHD-based magnetosheath values at the nearby seed points. The next section describes how we extracted the MHD-based values at each seed grid.

2.2   Parameterization of MHD Model

Open Geospace Global Circulation Model (OpenGGCM) global magnetosphere−ionosphere MHD model was used to extract MHD-based magnetosheath values as a function of solar wind/IMF conditions. OpenGGCM solves a semi-conservative form of the MHD equations in a stretched 3D Cartesian grids. The semi-conservative form means that OpenGGCM numerically conserves mass, momentum, and plasma energy, but not the total energy, to avoid instability arising when forcing a fully conservative form (Raeder et al., 2008). OpenGGCM inputs solar wind and IMF conditions and outputs are plasma density, velocity, temperature, and electromagnetic fields in the simulation domain. This study used a standalone OpenGGCM model, ranging (−500, 25), (−48, 48), and (−48, 48) $R_{{{\mathrm{E}}}}$ for x, y, and z directions in the GSE coordinates. Model details and applications can be found in Raeder et al. (2001, 2008), Connor et al. (2012, 2014, 2015, 2016, 2021), Oliveira and Raeder (2015), Ferdousi and Raeder (2016), Ferdousi et al. (2021), Cramer et al. (2017), Jensen et al. (2017), Shi Y et al. (2017), and Kavosi et al. (2018).

Magnetosheath parameters change in response to solar wind (SW) and IMF conditions. For this project, we tested a total of 14 SW/IMF conditions: seven solar wind plasma number densities at 1, 5, 10, 15, 20, 25, and 30 cm$^{-3}$ and two IMF $B _z$ at −4 and 4 nT. Other SW/IMF parameters stay constant, IMF $B_x$ = $B _y$ = 2 nT, solar wind velocity $V _x$ = 400 km/s, $V _y$ = $V_z$ = 0 km/s, and temperature T = 10$^5$ K. The dipole tilt angle was set at zero.

For each SW/IMF condition, we determined the MP and BS locations within the MHD simulation, using maximum and minimum gradients of plasma density along a radial direction. We focused only on the dayside magnetosheath ($X_{{{{\mathrm{GSE}}}}}$ > 0) because soft X-ray emissions are stronger in the dayside magnetosheath (Connor et al., 2021). Also, for simplicity, we don't consider the polar cusp impact on an MP shape, i.e., no dips near the cusps. When finding the MP location with density gradients, we forced the radial distance between nearby MP points to be less than 0.8 $R_{{{\mathrm{E}}}}$ for a smooth MP shape near polar cusps. After the magnetosheath boundaries are determined, we set up the seed grids for our magnetosheath model, with a spatial resolution of 0.1 in the fractional distance f and 1° in $\theta$ and $\phi$. Finally, we read the modeled magnetosheath parameters at every grid and save them as the database for our MHD-based model in Mshpy23. These grid values are linear interpolated to obtain magnetosheath parameters at a location given by a user.

2.3   Comparison with THEMIS Statistics

The THEMIS mission was launched in 2007 into highly elliptical and nearly equatorial orbits for studying magnetospheric substorms. A total of five THEMIS satellites cover vast areas of the Earth’s magnetosphere, providing crucial information of the Sun−Earth interactions. This study utilized 7 years of THEMIS magnetosheath observations (2007–2014) published in Dimmock et al. (2017). They conducted a statistical study of the dayside magnetosheath conditions, using 3-min averages of THEMIS Fluxgate Magnetometer (FGM) and Electrostatic Analyzer (ESA) data that are matched with the 20-min averages of OMNI solar wind/IMF conditions before each THEMIS data point. By averaging the THEMIS and OMNI data, their dataset not only suppresses small-scale transient effects in the magnetosheath and solar wind but also includes solar wind propagation effect from the BS nose to the THEMIS locations in the magnetosheath. Dimmock et al. (2017) calculated the BS and MP position using models of Shue et al. (1998) and Verigin et al. (2001) with the 20-min average of OMNI data, and then obtained the Magnetosheath Interplanetary Medium (MIPM) coordinates of the corresponding THEMIS data point using the boundary information. MIPM is an extension of the Geocentric Interplanetary Medium (GIPM) reference frame (Verigin et al., 2006). In GIPM, axes are defined as follows:

where $t = {\boldsymbol{B}}\cdot\hat{X}_{{\rm{gipm}}}$. Then MIPM coordinates are defined as:

Note that THEMIS data points were collapsed to the equatorial plane by simple projection because THEMIS satellites have a nearly equatorial orbit. We used these THEMIS datasets in the MIPM coordinates and their corresponding OMNI data for the validation of our MHD-based magnetosheath model. The main difference between the coordinate system used in this paper and MIPM coordinates is that the latter organizes magnetosheath points based on the shock geometry, either Parker spiral or ortho-Parker spiral. This difference may affect the comparison of plasma properties between the two coordinate systems. We acknowledge this issue and plan to incorporate MIPM coordinates into our model in the next version to provide a more accurate description of the plasma properties in the interplanetary medium, particularly in cases where the shock geometry may have a significant impact on plasma properties.

From the THEMIS and OMNI data set of Dimmock et al. (2017), we estimated average magnetosheath conditions for the 12 solar wind/IMF conditions used in our magnetosheath model. We first selected the THEMIS data when solar wind and IMF satisfy the following conditions: 0 < $B _x$ < 4 nT, 0 < $B_y$ < 4 nT, 300 < $|V|$ < 500 km/s. Then, we further down-selected the THEMIS data to match each solar wind/IMF condition. For IMF $B_z$ = 4 and −4 nT, we selected the THEMIS observations during IMF $B _z$ = 2–6 and from –6 to –2 nT, respectively. For solar wind plasma density ($N_{{\mathrm{sw}}}$) at 5, 10, 15, 20, 25, and 30 cm$^{-3}$, we selected the THEMIS observations when $N _{{\mathrm{sw}}}$ ranges between 0–10, 5–15, 10–20, 15–25, 20–30, and 25–35 cm$^{-3}$, respectively. Finally, the selected THEMIS data for each solar wind/IMF condition were bin-averaged with the resolution of 0.1 in f and 7.5° in $\phi$. The total number of THEMIS data points used in our study is ~224,000. However, some bins have very low counts. For $N_{{\mathrm{sw}}}$ > 25 cm$^{-3}$, 87% of the bins had less than 10 counts, thus making it difficult to obtain statistical magnetosheath conditions. In this study, we compared our MHD-based model results with the THEMIS magnetosheath data only for the conditions of solar wind density below 25 cm$^{-3}$, and only on the dayside.

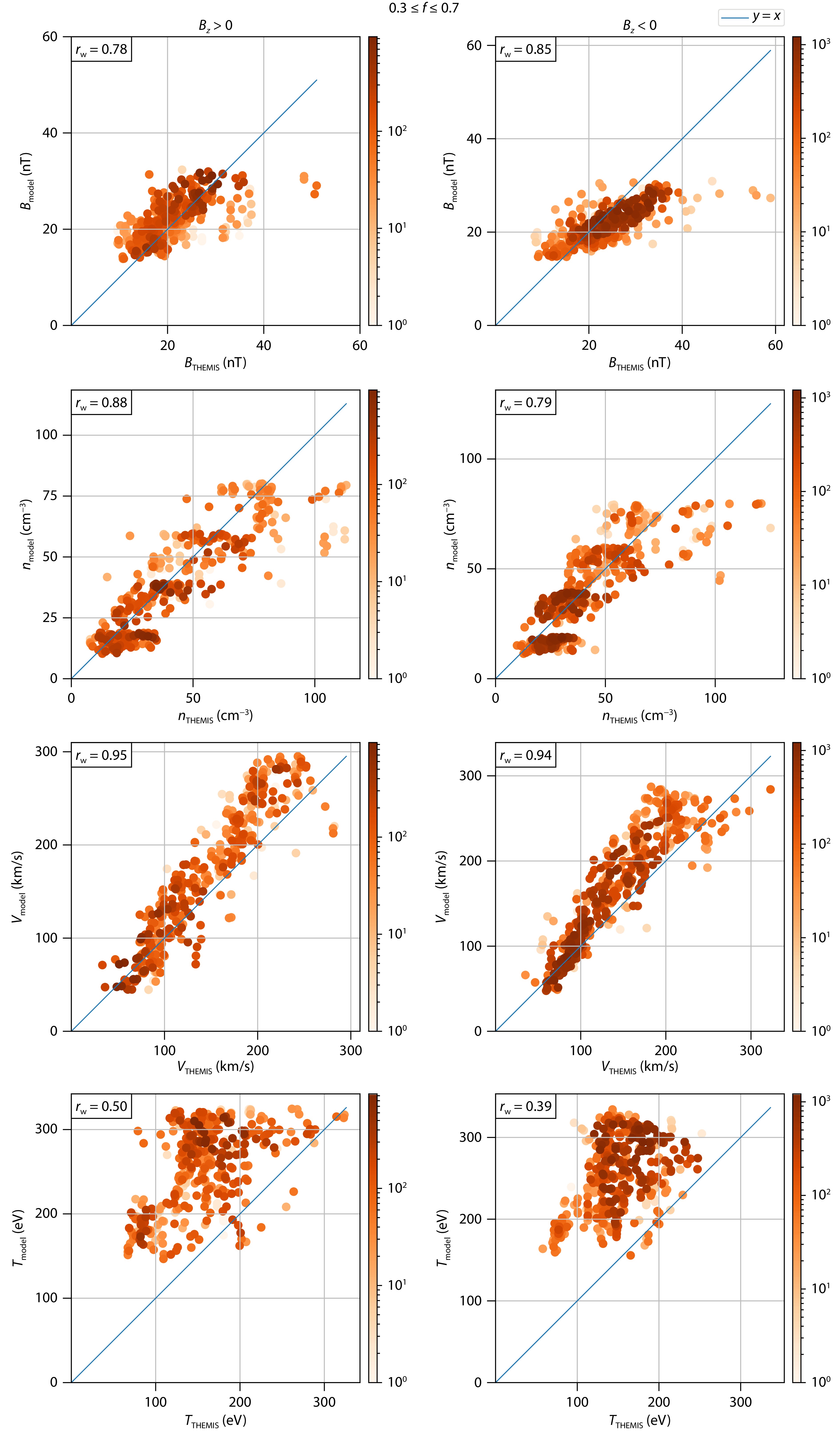
Figure 2 compares the MHD-based magnetosheath model results with the THEMIS statistical data for northward (left) and southward (right) IMF. From top to bottom, magnetic field magnitude, plasma density, plasma speed, and temperatures are shown. In this figure, we used only the THEMIS data within f = 0.3–0.7 because the THEMIS data points of f < 0.3 or f > 0.7 can be affected by the motion of the bow shock and magnetopause and thus are prone to errors. In reality, this means these bins can be mixed with the magnetosphere or solar wind data, thus potentially contaminating the statistical analysis of magnetosheath conditions. Darker red dots mean that the THEMIS data points are statistically strong. The blue line is the y = x reference line. All the data points will be aligned with this blue line if our model results perfectly match with THEMIS statistical data. The upper left corners show the weighted Pearson correlation coefficients ($r_{\mathrm{W}}$). Here, weights are based on the number of THEMIS bin counts so that the statistically insignificant data points are penalized in the $r _{\mathrm{W}}$ calculation.

Figure  2.  Comparison between the THEMIS statistical magnetosheath data and the MHD-based magnetosheath model results for IMF $B_z$ = 4 nT (left) and –4 nT (right). THEMIS data for IMF $B_z$ = 2–6 nT and from –6 to –2 nT are used for obtaining statistical magnetosheath conditions for IMF $B _z$ = 4 and –4 nT, respectively. From top to bottom, magnetic field magnitude, plasma density, plasma speed, and temperature are shown. Colors represent the number of THEMIS bin counts used in the calculation of averaged magnetosheath parameters. Blue lines represent the perfect model-data match lines. The upper left corner shows the Pearson correlation coefficient ($r_{\mathrm{W}}$) weighted by the number of THEMIS bin counts.

DownLoad: Full-Size Img PowerPoint

Plasma density, speed, and magnetic field magnitude in Figure 2 shows a Pearson correlation coefficient larger than or equal to 0.78 for both southward and northward IMF cases. Our data points are not perfectly aligned with the blue line, but this is understandable considering the following issues in the THEMIS dataset. First, transient structures like Kelvin-Helmholtz instability and mirror modes in the magnetosheath might modify statistical average of plasma properties. Second, the uncertainty in the solar wind propagation (Sivadas and Sibeck, 2022) may cause mismatch when pairing OMNI data with THEMIS data. Third, the empirical models of MP (Shue et al., 1998) and BS (Verigin et al., 2001) can locate the boundaries different from reality, and thus THEMIS data points may falsely fall into different bins (i.e. $f$ and $\phi$). Fourth, the statistical magnetosheath data are gathered when SW and IMF are close to — not exactly at — a given upstream condition. On the other hand, the MHD-based magnetosheath data are obtained when the upstream values are exactly same as the given conditions for at least 20 minutes. Lastly, some bins still have low counts to determine average magnetosheath conditions. Despite these uncertainties in the statistical THEMIS dataset, our model-data comparison shows remarkably good agreement. We also see outliers, the data points largely deviated from the expected correlations, in the magnetic field and density plots of Figure 2. These data points are typically associated with the extreme driving conditions like interplanetary coronal mass ejections (ICMEs). The large magnetic field and density of the upstream solar wind during ICMEs can cause strong compression of the magnetosheath and creates abnormally large values in the THEMIS observations. Thus, we advise caution to users when using the Mshpy23-MHD model for such rare conditions.

Unlike the aforementioned magnetosheath parameters, the ion temperature shows a large discrepancy. There are several physical explanations for this. First, the default solar wind temperature used in OpenGGCM is 10$^5$ K, different from the typical solar wind temperature of 3 $\times$ 10$^4$ K (Dimmock and Nykyri, 2013). Considering this difference of solar wind temperature, it is not surprising that our modeled magnetosheath reveals higher temperatures than the observations. Second, the global MHD model does not address full dynamics in the magnetosheath and its surrounding areas. Magnetosheath temperature is heavily influenced by numerous kinetic processes such as magnetic islands, turbulent reconnection, ion-scale waves and turbulence, and magnetosheath jets (Karimabadi et al., 2014). In addition, the magnetosheath temperature is usually anisotropic, controlled by instabilities such as the mirror mode, firehose, and ion cyclotron, which maintain the magnetosheath plasma to marginal stability (Soucek et al., 2015). Since these processes are omitted in the global MHD model, it is understandable to see the disagreement between modeled and observed temperatures. Therefore, we advise users of our magnetosheath model to use our temperature results with caution. This temperature discrepancy could be improved in future by employing kinetic hybrid models but this is beyond a scope of the present work.

3.   Mshpy23: Compilation of Magnetosheath Models

3.1   Additional Magnetosheath Models

The previous section introduced the MHD-based magnetosheath model, a default model of Mshpy23. The Mshpy23 code includes three additional magnetosheath models in previous literature so that users can choose or compare various models of their interest. The first model is Mshpy23-Spreiter, based on Spreiter et al. (1966) that calculated plasma density, velocity, and temperature of the magnetosheath in terms of upstream solar wind parameters under hydrodynamics. The magnetosheath model of Spreiter et al. (1966) have been widely used and have shown good agreement with in-situ space observations (see the review of Stahara, 2002). Soft X-ray physicists have also utilized this model for calculating near-Earth soft X-ray emissions (e.g., Robertson and Cravens, 2003; Carter et al., 2010). We obtained a file used in Carter et al. (2010) that parameterizes the model results of Spreiter et al. (1966). The file includes the solar wind versus magnetosheath ratios of plasma density and velocity as a function of magnetosheath locations so that the two magnetosheath parameters are obtained by simply multiplying the ratios to the upstream solar wind parameters. The magnetosheath temperatures are then calculated by equation 28 of Spreiter et al. (1966). We read the ratio of Spreiter et al. (1966) using the same magnetosheath grids ($f$, θ, $\phi$) as the Mshpy23-MHD model and used the ratios as seed parameters. We also adopted Shue et al. (1998) and Jelínek et al. (2012) boundary models for Mshpy23-Spreiter, instead of outdated boundary models in Spreiter et al. (1966). We compared the Mshpy23-Spreiter results with the THEMIS statistical data (not shown in our paper) and found that performance of this gasdynamic model is comparable to the Mshpy23-MHD model.

The second magnetosheath model is Mshpy23-RV from Romashets and Vandas (2019) that calculates only magnetic field vectors in the magnetosheath as a function of IMF and solar wind dynamic pressure. Their model is an improved version of Kobel and Flückiger (1994). Kobel and Flückiger (1994) model assumed that currents are concentrated at the magnetosheath boundaries (i.e. magnetopause and bow shock), and that inside of magnetosheath is current-free, i.e. $\nabla\times{\boldsymbol{B}} = 0$. Subsequently, magnetosheath magnetic field (${\boldsymbol{B}}$) can be expressed as magnetic potential ($\phi_B$), ${\boldsymbol{B}} = \nabla\phi_B$, satisfying the Laplace equation, $\nabla^2\phi_B = 0$. For simplicity, they assumed that magnetopause and bow shock are confocal paraboloids. Romashets and Vandas (2019) improved the magnetosheath boundary models by using the BS model of Formisano (1979) and the MP model of Formisano et al. (1979), allowing non-confocal shape of magnetosheath boundaries. The requirement of Romashets and Vandas (2019) model for the boundary models are they should be able to be described in parabolic equation with standoff distances and foci for the MP(BS). We used Jelínek et al. (2012) MP/BS models as they satisfy the requirements, and also Vandas et al. (2020) used these boundary models for applying Romashets and Vandas (2019) model.

The third magnetosheath model is Mshpy23-SE from Soucek and Escoubet (2012) and provides only magnetosheath plasma velocity with solar wind velocity input. Their model utilized the idea of Kobel and Flückiger (1994) that when IMF is nearly parallel to the solar wind flow, magnetic field lines can be considered as plasma stream lines. Soucek and Escoubet (2012) inputted the direction of solar wind velocity as the IMF direction, solved magnetic potentials following Kobel and Flückiger (1994), and obtained the magnetic field lines as a proxy of plasma stream lines. The plasma velocity directions are obtained from the stream lines. The magnitude of plasma velocity is obtained by solving the Rankine-Hugoniot relation and the continuity equation with an adhoc model of plasma density. In the model density $\rho$ at a fractional distance $f$ is related to the density on the same flowline near the shock $\rho_{\mathrm{d}}$ as: $\rho/\rho_{\mathrm{d}} = 0.8+0.2\times {\mathrm{tanh}}(4f)$. Soucek and Escoubet (2012) used the BS model of Farris et al. (1991) and the MP model of Shue et al. (1998). In contrast to the time-averaged flaring parameter used in Farris et al. (1991) BS model, Mshpy23-SE incorporated the BS model developed by Jelínek et al. (2012). This implementation enables the BS location and shape to dynamically adjust to varying SW/IMF conditions.

Instead of using time-averaged flaring parameter of Farris et al. (1991) BS model, Mshpy23-SE implemented the BS model of Jelínek et al. (2012), allowing the BS location changes under various solar wind/IMF conditions.

The Mshpy23 code also allows users to manually adjust MP and BS locations. If spacecraft observes the magnetosheath boundaries at different locations than the Mshpy23 MP/BS models, users can radially move the model boundaries to match with the observed boundary locations. The examples are shown in Section 3.1.

3.2   Comparison with Satellite Magnetosheath Crossing

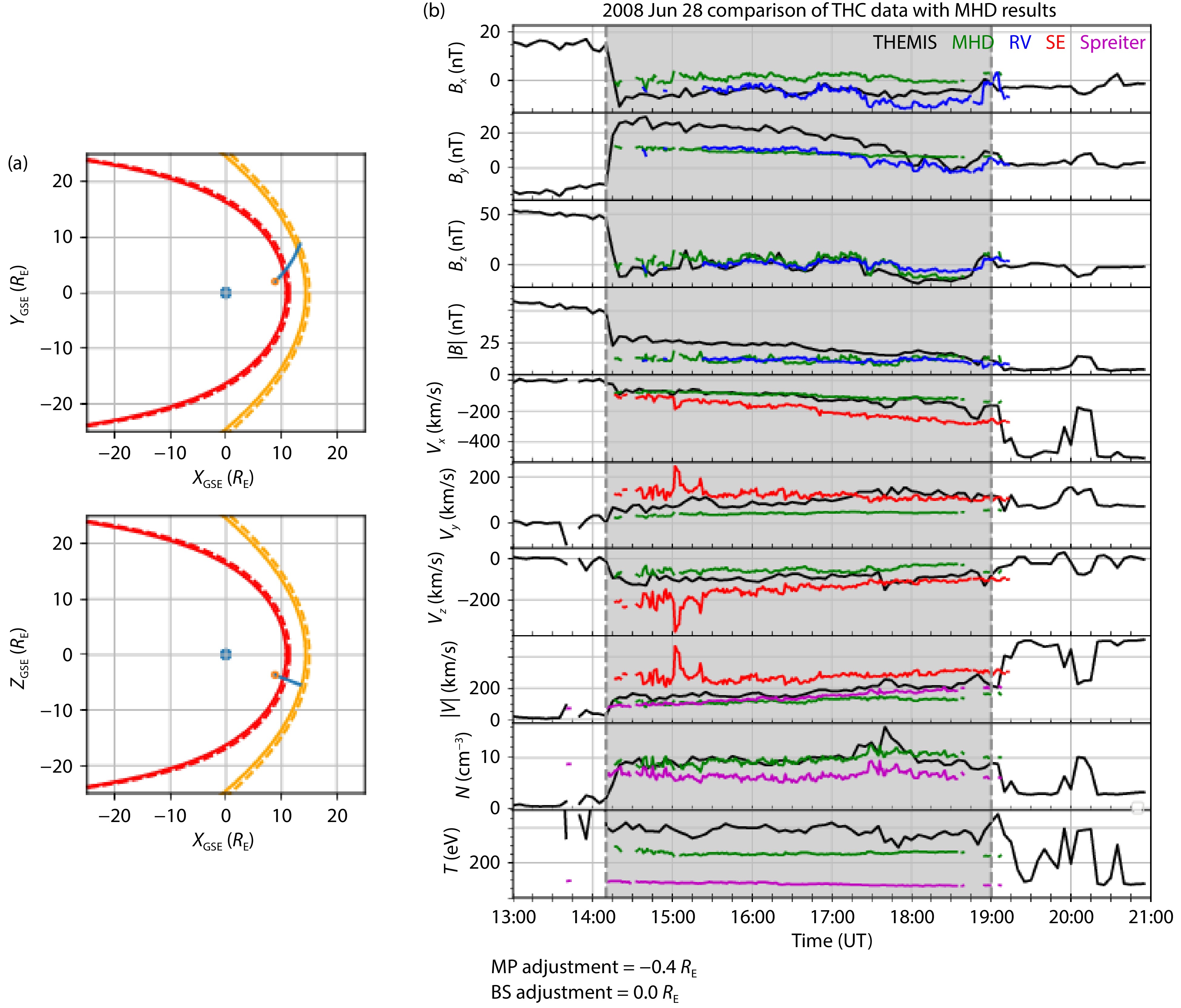
We conducted an analysis of two magnetosheath crossing events by comparing the Mshpy23 results with satellite observations. The first event involved the crossing of the magnetosheath by the THEMIS C satellite on June 28, 2008. Figure 3a shows the location of the satellite during the event, projected on the GSE XY (top) and XZ (bottom) planes. The satellite was in the magnetosphere at 13:00 UT (orange dot) and moved to the upstream solar wind along the blue line after passing through the magnetosheath between 14:08 and 19:00 UT. To implement time-varying magnetosheath boundaries, we used the THEMIS C trajectory from NASA CDAWeb and SW/IMF conditions from NASA OMNI data (King and Papitashvili, 2005) as input for Mshpy23. It is important to note that for satellite crossings like this, we need SW/IMF conditions matched to the spacecraft position array to determine the magnetosheath boundaries corresponding to each spacecraft position.

Figure  3.  The magnetosheath crossing event on 28 June 2008. (a) THEMIS C orbit (blue) projected on the GSE XY (top) and XZ (bottom) planes. The starting location for THEMIS C is shown as an orange dot. Orange lines represent the BS locations at the start (solid) and the end (dashed) of the THEMIS event, calculated from Jelínek et al. (2012). Similarly, red lines are the MP locations at the start (solid) and the end (dashed) of this event, calculated from Shue et al. (1998) model. (b) Model-data comparison of magnetosheath parameters. The THEMIS C observations (black) are compared with the MHD-based magnetosheath model (green), the Romashets and Vandas magnetic field model (blue), the Soucek and Escoubet plasma velocity model (red), and the Spreiter gas-dynamic model (purple). Magnetic field $B_x$, $B_y$, $B_z$, $|B|$, plasma velocity $V_x$, $V_y$, $V_z$, $|V|$, number density, and temperature are shown from top to bottom. The gray shaded area indicates when THEMIS passes through the magnetosheath.

DownLoad: Full-Size Img PowerPoint

To match the THEMIS magnetopause crossing data, we manually shifted the Shue MP by 0.5 $R_{\mathrm{E}}$ earthward for the entire duration. In Figure 3b, we compare the Mshpy23 model results with the THEMIS C observations (black). The green, blue, red, and magenta lines represent the MHD-based magnetosheath model (Mshpy23-MHD), the Romashets and Vandas magnetic field model (Mshpy23-RV), the Soucek & Escoubet plasma velocity model (Mshpy23-SE), and the Spreiter gas-dynamic magnetosheath model (Mshpy23-Spreiter), respectively.

In Figure 3, both Mshpy23-MHD and Mshpy23-RV results show good agreement with the THEMIS $B_z$ observations. Mshpy23-MHD predicts number density better than Mshpy23-Spreiter and plasma velocity (namely, $V_x$, $V_y$, and $\lvert V\rvert$) better than Mshpy23-SE model. As expected, Mshpy23 shows large discrepancy in temperature because both Mshpy23-MHD and Mshpy23-Spreiter are based on fluid approaches and thus omit full kinetic processes that affect a magnetosheath temperature. Overall, Mshpy23-MHD performs reasonably well compared to other magnetosheath models. Additionally, Mshpy23-MHD satisfies self-consistency among all the magnetosheath parameters to some extent since its seed data are calculated under the MHD theory.

The second example event is the Cluster magnetosheath crossing on 4 May 2003, which was used in Connor and Carter (2019) for the analysis of near-Earth soft X-ray emission. As seen in the Figure 4a Cluster 4 was located in the magnetosheath at 08:00 UT (orange dot) and crossed the magnetosheath along the blue line during 11:50−13:10 UT before entering the upstream solar wind. Figure 4b compares the modeled magnetosheath parameters with the Cluster observations (black) in the same format as Figure 3b. Here we shifted MP by 0.9 $R_{\mathrm{E}}$ sunward and BS by 1.2 $R_{\mathrm{E}}$ earthward to match with observed Cluster boundary crossings. The modeled magnetosheath values are obtained after adjusting the boundaries. Similar to the THEMIS event, the Mshpy23-MHD predicts magnetosheath parameters better or comparable to the other magnetosheath models.

Figure  4.  The magnetosheath crossing event on 4 May 2003 in the same format of Figure 3. (a) Cluster 4 orbit projected on the GSE XY (top) and XZ (bottom) planes. (b) Model-data comparison of magnetosheath parameters.

DownLoad: Full-Size Img PowerPoint

4.   Modeling of Soft X-ray image

4.1   Soft X-ray Image Calculation

Soft X-ray is emitted when a highly charged solar wind ion steals an electron from an exospheric neutral and the electron moves to a lower energy state. This process is called "Solar Wind Charge Exchange (SWCX)". The SWCX source ions in solar wind include ${\mathrm{C}}^{6+}$, ${\mathrm{N}}^{6+}$, ${\mathrm{N}}^{7+}$, ${\mathrm{Ne}}^{9+}$, ${\mathrm{S}}^{10+}$, ${\mathrm{O}}^{7+}$, and ${\mathrm{O}}^{8+}$. They produces a variety of soft X-ray emission lines in the energy of 0.4−1.0 keV.

LEXI and SMILE will have an soft X-ray instrument on board, visualizing the dayside magnetospheric system in soft X-ray. The Earth’s magnetosheath emits strong soft X-rays because solar wind ions are densely populated in the magnetosheath. Soft X-ray imaging of the magnetosheath enables us to capture the magnetopause motion (Collier and Connor, 2018; Sun TR et al., 2019; Jorgensen et al., 2019) and thus unveil reconnection modes under time-varying SW/IMF conditions. To support mission planning and data analysis of LEXI and SMILE, we developed a simple Mshpy23-Xray tool that simulates soft X-ray images expected from various vantage points under different upstream conditions.

The SWCX energy flux along a line of sight for a single emission line is given by the following equation (Kuntz, 2019):

where $E$ is a photon energy emitted after the charge exchange, $n_{\mathrm{n}}$ is a neutral density, n is an ion density of a certain charge state (e.g., ${\mathrm{O}}^{7+}$), and $v_{{\mathrm{rel}}}$ is a relative velocity between the ion and the neutral. Exospheric neutrals are originated from the upper atmosphere whose energy (or temperature) is $\sim$0.1 eV (Qin JQ and Waldrop, 2016). It is expected that exospheric neutrals are much slower than the magnetosheath plasmas whose energy ranges rom several hundreds eV to a few keV. Neutral velocity is negligible in solar wind charge exchange. Assuming a negligible neutral velocity, $v_{{\mathrm{rel}}}$ can be approximated as a plasma velocity:

where $v_{\mathrm{r}}$ is an ion bulk velocity, and $v_{\mathrm{t}}$ is an ion thermal velocity, $v_{\mathrm{t}} = \sqrt{(3kT/m_{\mathrm{p}})}$. $\sigma(v_{{\mathrm{rel}}})$ is a charge exchange cross section and depends on $v_{{\mathrm{rel}}}$. $b$ is a probability of emission after SWCX. d$\Omega$ is a solid angle that corresponds to an X-ray image resolution. The integral is done along the line of sight distance $s$, from $s = 0$ to $s = \infty$.

Equation (12) can be simplified by grouping the parameters provided by Mshpy23 and applying several assumptions. Here we define a potential reaction rate Q:

where $n_{\mathrm{p}}$ is a solar wind proton density. Hydrogen atoms are the most dominant species in the exosphere above 1500 km altitude (Zoennchen et al., 2022). We used the following exospheric density model of Cravens et al. (2001):

with neutral density at 10 $R _{\mathrm{E}}$, $N_0$ = 25 cm$^{-3}$, n_n is in $\rm{cm}^{-3}$ . Then, the Equation (12) is written as:

Following Schwadron and Cravens (2000) and Pepino et al. (2004), we assumed that the atomic parameters ($\sigma$, $b$) and abundance ratio $n/n_{\mathrm{p}}$ is constant along a line of sight. Then total energy flux for a certain energy band [$E_1$, $E _2$] can be written as

where

An effective scale factor ($\alpha$) combines abundance, cross section and emission probability of solar wind ion species including C, N, Ne, S, and O. Abundance can be determined from the in-situ measurements of solar wind ions, e.g. data from the Advanced Composition Explorer (ACE) Solar Wind Ion Composition Spectrometer (SWICS) (Whittaker and Sembay, 2016). Other parameters ($E_j$, $\sigma$, and $b$) can be theoretically and/or experimentally obtained (Betancourt-Martinez, 2017). However, due to the limitations of observations, theory, and experiment, exact alpha values are not fully understood and still under active studies. Here we adopt $\alpha$ = 6.0 × 10$^{-16}$ eV cm$^2$, following Cravens et al. (2001).

4.2   Example of Image Calculation

We calculated soft X-ray images during steady upstream conditions of solar wind density at 10 cm$^{-3}$, velocity at (400, 0, 0) km/s, temperature = 10$^5$ K, and IMF ${\boldsymbol{B}} = (2, 2, -5)$ nT in GSE coordinates. Figure 5a and 5b show X-ray emissivity rates ($P = \alpha n_{\mathrm{n}} n_{\mathrm{p}} v_{{\mathrm{rel}}}$) on an equatorial plane calculated from Mshpy23-Xray and a simple emissivity model of Jorgensen et al. (2019), respectively. The minimum and maximum emission rates are labeled at the bottom. Mshpy23-Xray first defined the magnetosheath boundaries of Shue et al. (1998) and Jelínek et al. (2012), obtained magnetosheath parameters from Mshpy23-MHD, and finally calculated X-ray emission rates on the equatorial plane as seen in Figure 5a. Jorgensen et al. (2019) introduces the following formula of soft X-ray emission rate:

Figure  5.  (a) Magnetosheath X-ray emission on the XY plane computed from Mshpy23-Xray and (b) Jorgensen et al. (2019) emission model. Both cases used Jeřáb et al. (2005) MP model and Jelínek et al. (2012) BS model for magnetosheath boundaries. (c) Soft X-ray emissivity map calculated from Mshpy23-Xray by locating a virtual spacecraft at $(X, Y, Z)_{{\mathrm{GSE}}}$ = (0, 30, 0) $R_{\mathrm{E}}$, (d) and $(X, Y, Z)_{{\mathrm{GSE}}}$ = (0, 0, 30) $R_{\mathrm{E}}$. The images use 0.25° × 0.25° angular resolution. Note that our model does not support the cusp structure. For all the models used for images, IMF was set to $\boldsymbol{B}=(2,2,-5)$ nT. Solar wind velocity was set to 400 km/s, solar wind density 10 cm$^{-3}$.

DownLoad: Full-Size Img PowerPoint

where a unit of $F(\boldsymbol{r})$ is eV cm$^{-3}$ s$^{-1}$, $\boldsymbol{r}$ points a location of interest, r is a geocentric distance of the location, and theta is an angel between $\boldsymbol{r}$ and the sun−earth line. $r_{{\mathrm{ref}}}$ = 10 $R_{\mathrm{E}}$. Jorgensen et al. (2019) fitted the parameters $A _1$, $A_2$, B, $\alpha$, and $\beta$ using a PPM (piecewise parabolic method)-MHD code simulation with following solar wind conditions: solar wind density n = 22.5 cm$^{-3}$; velocity $V_x$ = 400 km/s, $V_y$ = $V_z$ = 0; and interplanetary magnetic field $B_x$ = $B_y$ = 0, $B_z$ = 5 nT. Parameters fitted were $A_1$ = 3.2285 × 10$^{-5}$ eV cm$^{-3}$ s$^{-1}$, B = −1.7985 × 10$^{-5}$ eV cm$^{-3}$ s$^{-1}$, $\alpha_2$ = 2.4908, $\beta_2$ = −1.6458, $A _2$ = 1.3588 × 10$^{-5}$ eV cm$^{-3}$ s$^{-1}$, $r_{{\mathrm{ref}}}$ = 10 $R_{\mathrm{E}}$. For Figure 5b, we used the same boundary models of Mshpy23, i.e., Shue et al. (1998) and Jelínek et al. (2012).

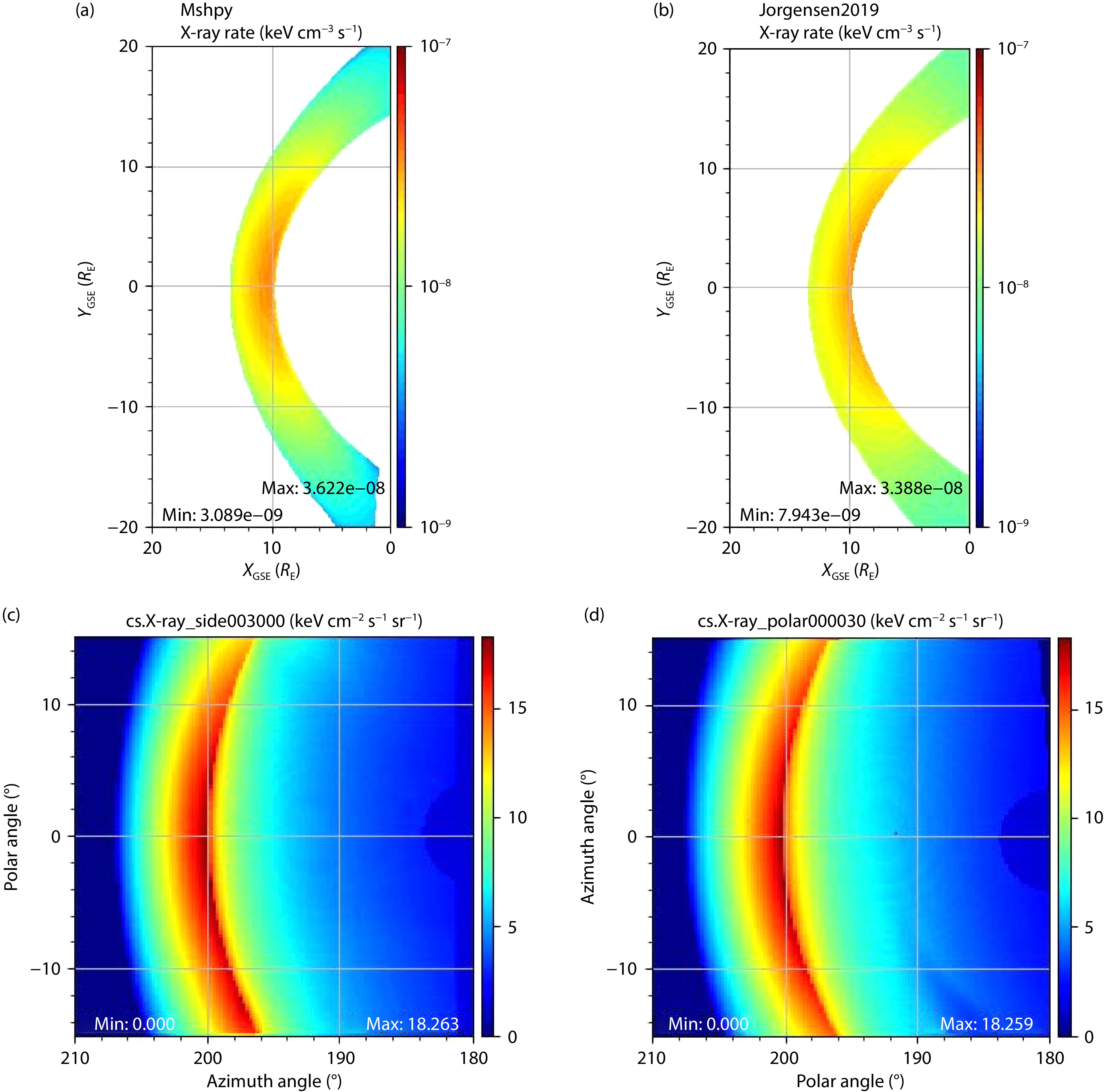
Figure 5a and 5b showed good agreement between the two emissivity models. Their emission rates are comparable. They are also stronger near a subsolar point and weakens as moving toward the flank. This is because less exospheric neutrals are available in the magneotsheath flank due to its long distance to the Earth’s upper atmosphere, the source region of exopsheric neutrals.

Figure 5c and 5d show soft X-ray images expected from two virtual spacecrafts at $(X, Y, Z) _{{\mathrm{GSE}}}$ = (0, 30, 0) $R_{\mathrm{E}}$ and (0, 0, 30) $R _{\mathrm{E}}$ and calculated from Mshpy23-Xray. The colors represents integrated X-ray emission rates along lines of sight within a 30° × 30° field of view, in a unit of keV cm$^{-2}$ s$^{-1}$ sr$^{-1}$. The image angular resolution is set at 0.25° × 0.25°. The blue circular areas in Figure 5c and 5d are the region surrounding the Earth (r < 2.1 $R_{\mathrm{E}}$), and no X-ray calculation is done in this region. As expected, our images show strong magnetosheath emissions and are comparable to the images in previous literature (Cravens et al., 2001; Walsh et al., 2016; Sibeck et al., 2018; Connor et al., 2021) that utilized a global MHD model for the image calculation. One caveat of our images do not show cusps, another strong X-ray source, because the current version of Mshpy23 does not include cusp features. This will be our future task.

Real X-ray images can be different from the ideal images in Figure 5c-5d because of other X-ray backgrounds in the sky (e.g., light sources, diffuse astronomical backgrounds, and heliospheric backgrounds) and instrument effects (e.g., intrumental background, Poisson noise, limited field-of-view, and instrument responses) (Sibeck et al., 2018; Jung et al., 2022). Figure 6 shows ideal (left) and realistic (right) images expected from the SMILE soft X-ray instrument (SXI). We used solar wind density of 10 cm$^{-3}$, velocity of (400, 0, 0) km/s, temperature of 10$^5$K, and IMF of (2, 2, −5) nT in GSE coordinates. The left figure in Figure 6 shows an ideal image of SMILE SXI calculated from Mshpy23-Xray, when SMILE is located at (3.5, −2.3, 17.1) $R_{\mathrm{E}}$ and SXI points at (3.5, −2.3, 0) $R_{\mathrm{E}}$ in GSE coordinates with a 16° × 27° FOV. The right figure shows a realistic X-ray image obtained from a SMILE SXI tool with the left figure as input. This tool is developed by the SXI instrument team, and not included in Mshpy23. This SXI tool processes input spatial maps by folding them through the instrument response to predict the total observed X-ray counts map for a specified integration time and energy band. Here we used 5 minutes exposure time. The instrument response is the telescope’s effective area, which varies with energy and angular position within the field-of-view. To the output map, Poisson noise is added, and the processed version is obtained by subtracting the predicted background model and correcting for the telescope vignetting function. The resulting foreground SWCX emission prediction has noise per pixel appropriate to the total input components and background subtraction process. The synthetic SXI image in Figure 6b still shows strong magnetosheath emission but with non-negligible noises. The SMILE Modeling Working Group (MWG) have been developing several image analysis tools that extract a magnetopause location from noisy soft X-ray images (e.g. see Samsonov et al., 2022). Such image analysis tools will help to extract the magnetopause motion under various upstream conditions and thus unveil dayside reconnection modes.

Figure  6.  (Left) Side-view of simulated soft X-ray emissivity map observed by SMILE at $(X, Y, Z)_{{\mathrm{GSE}}}$ = (3.5, −2.3, 17.1) $R_{\mathrm{E}}$. White rectangle is the assumed field-of-view of 16° × 27°. (Right) Simulated image processed with SMILE SXI tool.

DownLoad: Full-Size Img PowerPoint

5.   Model Limitation and Fut Work

In this section, we discuss future directions for improving Mshpy23. Firstly, we plan to enhance the model by including more SW/IMF conditions. As noted in Section 2.3, the current version of Mshpy23 did not account for the impact of various SW/IMF conditions, leading to a mismatch with observed data under high solar wind density conditions. Additionally, as seen in Figure 2, Mshpy23-MHD tends to overestimate temperature (average 1.662 times higher than THEMIS data). However, the primary focus of soft X-ray imaging is to accurately identify the MP position for studying reconnection mode, making the absolute magnitude of emission less critical. Instead, the model’s ability to precisely represent the boundary location and structure holds greater importance. To address these limitations and improve the model’s performance, we will incorporate OpenGGCM runs under multiple SW velocities, stronger/weaker IMF, various directions for IMF, and diverse SW temperatures. This comprehensive approach will enhance the accuracy of our model predictions under a wider range of SW/IMF conditions.

Secondly, our goal is to enhance the boundary prediction of Mshpy23 by incorporating more sophisticated models for the MP and BS. The current version of the model only includes testing a few simple MP/BS models, and we have not tested the Verigin et al. (2001) model, which was used in the compilation of our THEMIS dataset (Dimmock et al., 2017). We recognize that the rotational symmetry of the Jelínek et al. (2012) BS model may lead to inaccurate predictions for magnetosheath parameters, particularly in the flank regions. Therefore, we will address this limitation by incorporating additional boundary models, including the Lin RL et al. (2010) MP and Verigin et al. (2001) BS model. This expansion will provide our model users with more choices and options for representing the magnetosheath boundaries more accurately. For users who seek to use our model in actual event analysis, we advise complementing the model with in-situ measurement data from heliospheric satellite like THEMIS or MMS, as demonstrated in our adjustments in Section 3.2.

Thirdly, our plan includes the expansion of the model’s coverage to encompass the nightside magnetosheath domain. At present, the model is limited to the dayside magnetosheath domain with a longitude range of −90° < longitude < 90°. However, our objective is to extend the supported magnetosheath longitude range to approximately −120° < longitude < 120°. This expansion poses challenges because the current method of defining magnetosheath boundaries for Mshpy23-MHD seed grids, which relies on plasma density gradients along a radial direction, is not well-suited for the nightside magnetosheath. To overcome these challenges and validate the nightside magnetosheath data, we are exploring alternative methods for determining nightside MP and BS locations. One approach is to utilize data from other missions such as Geotail, Cluster, or MMS, which have the potential to provide valuable insights into the nightside magnetosheath conditions. By integrating data from these missions, we aim to improve the accuracy and reliability of the nightside magnetosheath representation in our model.

Fourthly, we will include the polar cusp region in Mshpy23. The current version of Mshpy23 does not take into account polar cusps that are strong emission regions of soft X-ray and ENA. The difficulty of modeling coordinates in the magnetosheath, including the polar cusp with its complex shape, results in a limitation to accurately represent points in this region with suitable coordinates. This, in turn, makes it challenging to model the cusp region in the magnetosheath modeling approach. However, we plan to include an analytic cusp model in the future version of Mshpy23.

Lastly, we plan to consider the dipole tilt effect in our model. The tilt of the Earth’s magnetic dipole axis with respect to the rotational axis creates an asymmetric magnetopause shape (Samsonov et al., 2016). Although the dipole tilt impact on the magnetosheath parameters are not well understood, this limitation could affect the accuracy of the Mshpy23 predictions. Therefore, we plan to test the dependence of Mshpy23 on dipole tilt to improve the accuracy of our predictions.

We aim to enhance the model-data validation process by incorporating a more extensive set of in-situ observations spanning the entire magnetosheath region and creating statistically robust data samples. However, the current THEMIS dataset utilized in this study is limited to magnetosheath parameters near the equatorial region, constrained by its orbit. Additionally, the distribution of data points among the magnetosheath bins is uneven, leading to statistically inadequate bin-averages. Notably, about 47% of total bins (1174 bins) contain fewer than 10 data points, resulting in limited statistical representation.

To address these limitations and improve our model validation, we plan to include magnetosheath observations from the Cluster and MMS missions. By incorporating data from these missions, particularly during special conjunctions where Cluster, MMS, and THEMIS all traverse the magnetosheath simultaneously, we can expand the data coverage to higher latitude and obtain more comprehensive and representative samples for model validation. The analysis of data from these special conjunctions, alongside comparisons to the OpenGGCM MHD model, will enable us to enhance the precision and reliability of our current model. Integrating data from multiple sources will offer a more robust validation framework and provide a more comprehensive understanding of the magnetosheath’s dynamics and behavior across various spatial regions.

6.   Summary

We developed a Mshpy23 Python tool that calculates plasma density, velocity, temperature, and magnetic fields of the magnetosheath with solar wind and IMF input. This tool includes four different models: the MHD-based model newly developed in this paper, the gas-dynamic model of Spreiter et al. (1966), the magnetic field model of Romashets and Vandas (2019), and the velocity model of Soucek and Escoubet (2012) that are named Mshpy23-MHD, Mshpy23-Spreiter, Mshpy23-RV, and Mshpy23-SE, respectively.

Figure 7 shows a schematic diagram of Mshpy23. First, a user inputs a position in the magnetosheath and SW/IMF conditions at a bow shock nose in the GSE coordinate system. The input position can be an array of various dimensions such as a satellite trajectory, 2D grids on equatorial/meridional planes, and 3D grids of global magnetosheath. The SW/IMF input can also be an array if the input position is given as a time-varying array (e.g., a satellite trajectory). Second, Mshpy23 obtains MP and BS locations using Shue et al. (1998) and Jelínek et al. (2012) as default models, except the Mshpy23-RV. Romashets and Vandas (2019) magnetic field model requires parabolic MP shape, so Shue et al. (1998) MP model cannot be used. Following Vandas et al. (2020), we used Jelínek et al. (2012) MP model for the Mshpy23-RV. Mshpy23 provides an option to use another BS model of Jeřáb et al. (2005) by entering a desired BS model name as input. As shown in Section 3.2, a user can adjust MP/BS positions radially with an optional input to Mshpy23 for matching the boundaries with satellite observations. Third, Mshpy23 calculates magnetosheath parameters from a selected magnetosheath model among Mshpy23-MHD, Mshpy23-Spreiter, Mshpy23-RV, and Mshpy23-SE. Finally, in case that the input positions are 2D or 3D arrays, Mshpy23-Xray can calculate the 2D cut of X-ray emissivity or the soft X-ray images seen from a virtual spacecraft. Mshpy23-Xray uses Mshpy23-MHD as a default magnetosheath model.

Figure  7.  Schematic diagram of Mshpy23.

DownLoad: Full-Size Img PowerPoint

Mshpy23-MHD is constructed from 14 OpenGGCM simulations under seven solar wind densities of 1, 5, 10, 15, 20, 25, and 30 cm$^{-3}$ and two IMF $B _z$ components of −4 and 4 nT. The model results are compared with the THEMIS statistical data from Dimmock et al. (2017). Plasma density, velocity, and magnetic field magnitudes showed good model-data agreement with weighted Pearson coefficients larger than 0.78. However, the model tends to show higher temperature than the observations, because only one solar wind temperature were used in the OpenGGCM simulations and because MHD physics cannot address full heating mechanisms in the magnetosheath.

Mshpy23 also includes three additional magnetosheath models of previous literature. Mshpy23-Spreiter provides plasma number density, speed, and temperature, Mshpy23-RV provides only magnetic fields, and Mshpy23-SE provides only plasma velocities. We conducted model-data comparison for the magnetosheath crossing events of THEMIS and Cluster and checked performance of all magnetosheath models in our tool. Mshpy23-MHD was on par with other magnetosheath models while satisfying self-consistency among magnetosheath parameters under MHD physics.

Mshpy23-Xray calculates a soft X-ray image of the dayside magnetosheath, using Mshpy23-MHD as a default magnetosheath model. By inputing a virtual sapcecraft position and SW/IMF conditions of interest, a user can produce an expected soft X-ray images without sophisticated knowledge of a gloabl MHD model. Our X-ray images show good agreement with the ones in previous literature (Jorgensen et al., 2019; Connor et al., 2021) except that cusp signatures are missing due to the current limitation of Mshpy23-MHD.

Mshpy23 is an user-friendly, open-source code that parameterizes global magnetosheath environment under various SW/IMF condtions. Mshpy23-MHD is an empirical magnetosheath model based on the MHD theory. It is upgraded from a widely used empirical model based on Spreiter et al. (1966). Mshpy23-Spreiter, Mshpy23-RV, and Mshpy23-SE also increase users' accessibility to other magnetosheath models without writing new codes from scratch. Finally, Mshpy23-Xray quickly reproduces soft X-ray images from various vantage points under different SW/IMF conditions without simulating a global magnetosphere model (e.g., MHD, hybrid, or particle-in-cell simulations). This will support the planning and data analysis of LEXI and SMILE soft X-ray instruments.