Influences of various space current systems on the geomagnetic field in near-Earth space

1.   Introduction

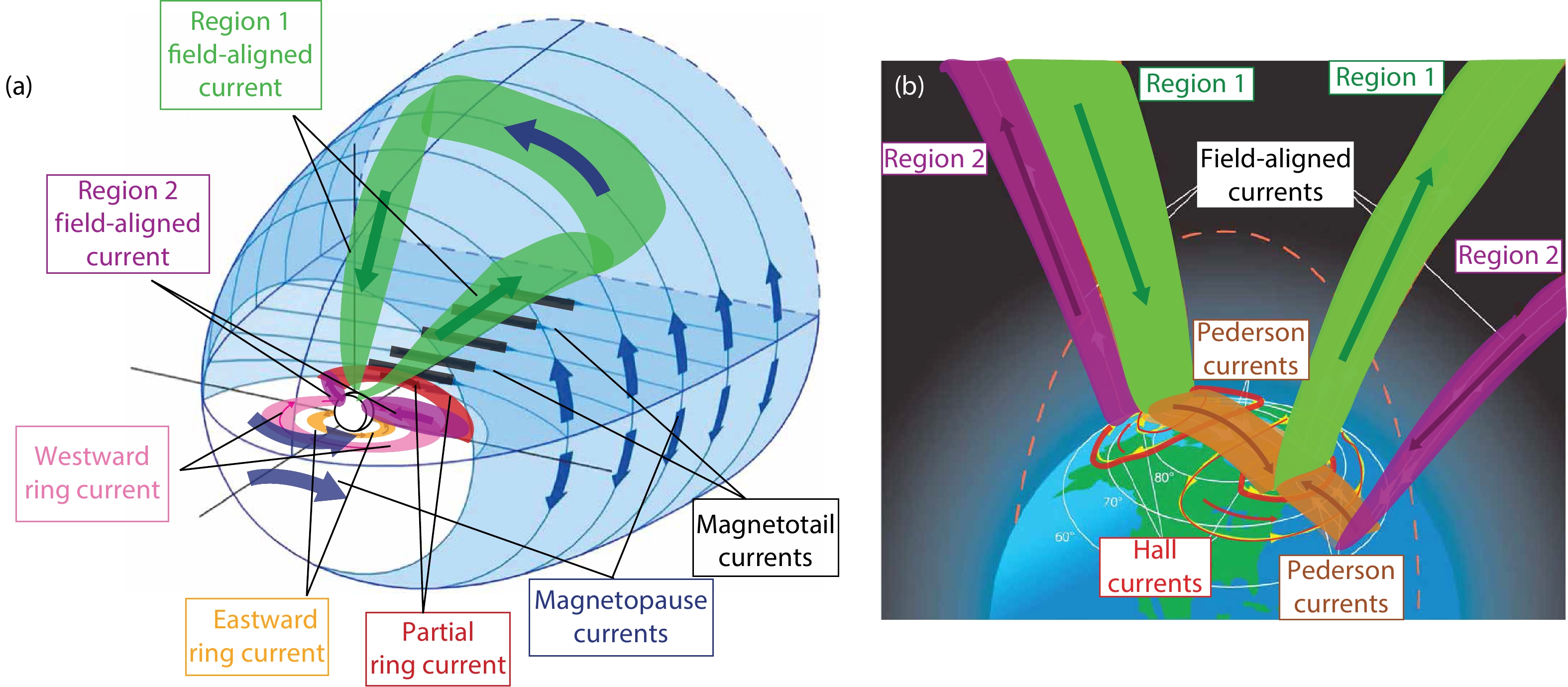
The Earth’s geomagnetic field acts as a shield to protect the planet’s surface from being bombarded by what would otherwise be a continuous stream of high-energy particles and cosmic rays. This protection has been a key factor in determining the characteristics of Earthly life forms. A variety of sources contribute to the near-Earth magnetic field. Internal sources, mainly in the planet’s core and lithosphere, contribute 97% of the total surface field (~30,000 nT at the equator and ~60,000 nT at the poles). The magnetosphere and ionosphere, the most important regions coupling the Sun and Earth, are strongly influenced by solar activity (such as flares and Coronal Mass Ejections (CME)), Interplanetary Magnetic Fields (IMF), geomagnetic disturbances, the planet’s seasons, and other factors. The interaction between charged particles and background electromagnetic fields in these regions produces a number of current systems, most notably the magnetopause currents (known also as Chapman−Ferraro currents), magnetotail currents, ring and partial ring currents, high latitude field-aligned Region 1 current and equatorward Region 2 current, Pedersen and Hall currents, Solar quiet (Sq) currents, Equatorial Electrojet (EEJ), meridional currents connecting the two hemispheres, and others. These currents, as well as the currents that they induce, constitute the complex external fields $\left(\nabla \times {\boldsymbol{B}}={\mu }_{0}{\boldsymbol{j}}\right)$, which account for about the remaining 3% of the total magnetic field near the Earth surface.

Accurately distinguishing among different field sources is important for understanding their physical processes and evolution. Therefore, different geomagnetic field models have already been proposed and studied. Traditional geomagnetic field models have tended to model each source separately; no previous model has attempted to model all major sources and their interactions. Under the assumption that field measurements are acquired in the current-free region, which means the curl of the B field is equal to zero, models of core, lithosphere, magnetosphere, and ionosphere have taken the form of gradients of Laplacian potential in spherical coordinate systems. Using ground-based observatory measurements, and observations collected by satellites (Swarm, Cryosat2, CHAMP, SAC-C, and Ørsted), CHAOS 7, the latest model in a series of time-dependent geomagnetic models developed by DTU, consists of the internal field up to degree 20, the LCS-1 lithospheric field model above degree 25, and an external field of degree 1 related to the Ring Current (RC) index (Olsen et al., 2006, 2014; Finlay et al., 2016, 2020). CM6, the culmination of a series of comprehensive models, coestimates contributions from all possible sources by analyzing the data from the Ørsted, SAC-C, CHAMP, and Swarm satellites, and from the ground observatory, and gives an external model of degree 60 (Sabaka et al., 2004, 2015, 2020). In addition, some models (such as MF7, EMM2017, and WMM) that simulate the contributions of different sources to different degrees. Although all of these models enjoy varying degrees of success in their ability to describe the target field in terms of its sources, they suffer at different levels of accuracy from their failure to take the underlying physical mechanisms into account. In addition, limited by polar orbits, traditional magnetic survey satellites cannot extract high-resolution east−west magnetic component data; these components play a very important role in building the comprehensive magnetic field model.

Macau Science Satellite-1 (MSS-1), the world’s first low-inclination equatorial geomagnetic survey satellite with 0.5 nT high-precision, will be launched in early 2023. By taking advantage of the MSS1’s improved temporal and spatial coverage of the Earth’s magnetic field and of the improved accuracy of its onboard instruments, it will be possible greatly to advance existing magnetic field models. The MSS1’s data, especially its measurements of the east and westward magnetic field components, will be invaluable to our further understanding of this crucial factor in making Earthly life possible.

In order to take full advantage of MSS-1, and to build an external model based on the physical formation mechanisms of different current systems by using the solar wind and interplanetary magnetic fields observed at 1 AU, we adopt the numerical simulations that have developed rapidly in recent years to self-consistently couple the solar wind, magnetosphere and ionosphere (De Zeeuw et al., 2004). For the first time, we study quantitatively the magnetic perturbation contribution of different current systems in space. Results show that numerical simulation can capture usefully the magnetic field disturbance characteristics of the main current systems, thus encouraging new ideas and providing a theoretical basis for refined geomagnetic field modeling in the near future.

The main structure of this article is as follows. In Section 2, the basic structure and dynamics of primary electric currents are presented and discussed. Section 3 covers basic principles of numerical simulation. In Section 4, simulation results of geomagnetic field perturbation due to relevant currents are given in detail. Finally, discussion and conclusions appear in Section 5.

2.   Magnetospheric and Ionospheric Currents

Interactions with the solar wind and ionosphere make the magnetosphere a highly dynamic region, within which a number of current systems and different energetical particle spectrums are formed (Smith and Hoffman, 1978; Ferradas et al., 2015; Wang YB et al., 2020; Zhang H et al., 2022). Understanding how these currents close and how these circuits change in time and space is important for revealing the dominant physical processes and for modeling external magnetic sources.

2.1   Chapman−Ferraro Magnetopause Currents

Based on the idea that the Earth’s internal geomagnetic field deflects the solar wind around it, Chapman and Ferraro (1932) suggested that the magnetosphere carves out a cavity in the solar wind; their idea was confirmed by Explorer 10 and 12 measurements (e.g., Cahill and Amazeen, 1963). A bow shock is formed in front of the supersonic solar wind when it hits the magnetosphere (Wang M et al., 2016, 2018; Lu JY et al., 2019). The boundary, also named magnetopause, separating the solar wind and the magnetosphere, is actually a current sheet, which can be understood by considering the gyration of proton and electrons in the magnetosheath, a region between the bow shock and the magnetopause. When protons and electrons move to regions with larger magnetic fields, they will return to the magnetosheath after half of the gyration. However, the opposite direction of gyration results in separation of positive and negative charges; that is, a net electric current flow occurs from dawn to dusk on the dayside, and from dusk to dawn across the high-latitude magnetopause (blue arrows as shown in Figure 1). The best illustration can be found in Kivelson and Russell (1995); their Fig. 9.1 shows that the magnetic perturbation due to this current can be sensed at the Earth’s surface, which will be shown in detail in Section 4.

Figure  1.  Schematic diagram of different current systems in the near-Earth space. Panel (a) presents the principal magnetospheric currents and coupling currents. PBlack arrows indicate the magnetotail currents; blue arrows indicate closure via magnetopause currents. Orange and pink arrows show the eastward and westward ring currents, respectively. Partial ring current and Region 2 field-aligned currents are shown in red and purple. Region 1 field-aligned current is shown in green. The Earth is the small sphere at the axis origin, and the Sun is to the left front. Panel (b) shows the ionospheric Pedersen (orange) and Hall (red) currents, as well as the Regions 1 (green) and 2 (purple) field-aligned currents. Revised from Ganushkina et al. (2018), and https://hamwaves.com/propagation.tutorials/doc/plates/ionospheric.currents.png.

DownLoad: Full-Size Img PowerPoint

2.2   Magnetotail Currents

Early in 1965, the discovery by Ness (Ness, 1965) of a long tail with stretched field lines on the nightside indicated a thin current sheet flowing from dawn to dusk near the equator out at 6.6 R_E (1 R_E is about 6378.140 km). This thin current sheet divides the magnetotail into two lobes with almost uniform magnetic fields in opposite directions, Earthward above this current, and anti-Earthward below it. This cross-tail current closes the loop with the tail magnetopause currents (shown in Figure 1 as black and blue arrows), forming the famous θ current structure seen from the magnetotail. Also, the instability of this current sheet plays an important role in the formation and evolution of substorms (e.g., Baker et al., 1996). Studies show that it is a persistent and stable system on a global magnetospheric scale.

2.3   Current Systems in the Inner Magnetosphere

Ring current systems, one of the oldest concepts in magnetospheric physics, were first proposed by Stormer (1907) and supported by Schmidt (1917). As observations increased, numerous studies reported the existence of a pressure peak around 3 R_E, inside which the pressure increases with the radial distance, and outside which the pressure decreases with the radial distance. According to the basic formation mechanism of the current $\left({{\boldsymbol{J}}}=\dfrac{{\boldsymbol{B}}\times \nabla P}{{B}^{2}}\right)$, that is, part of the magnetization current proportional to the pressure gradient contributes to the total current density, and part is canceled by the guiding center drift motion (Ganushkina et al., 2015). The B is the magnetic field, P is the particles’ pressure, and J is the total current density in the equation. Both the eastward (orange region as shown in Figure 1) and westward (pink region in Figure 1) ring currents exist inside and outside the pressure peak boundary. Observations show that these two ring currents are never purely symmetric (Jorgensen et al., 2004), which is inconsistent with the symmetric assumption in the geomagnetic modeling of ring currents. Also, the finding of the two magnetic field minima above and below the equator on the dayside greatly challenges the traditionally-assumed toroidal shape of the ring currents.

The partial ring current and its closure circuit were first proposed by Alfven in the 1950s (Egeland and Burke, 2012). As mentioned earlier, the magnetosphere is highly dynamic. Particle injections from the magnetotail into the inner magnetosphere will produce the azimuthal pressure gradient, which contributes to the asymmetry of the ring current, known also as the partial ring current (the red region around the nightside of the Earth as shown in Figure 1). The partial ring current shows more dependence on (i) the Kp index, which indicates the convection level of the mid-latitude magnetosphere, and on (ii) the Auroral Electrojet (AE) index, which captures mainly the high-latitude auroral activity. This is also the reason why the partial ring current connects preferably to the Region 2 field-aligned currents (the purple currents as shown in Figure 1).

2.4   Region 1 and Region 2 Field-aligned Currents

Birkeland current, named after their discoverer’s name, was first proposed by Birkeland in 1908 (Birkeland, 1908). This discovery as greatly advanced our understanding of polar physics. As shown in Panel (b) of Figure 1, the Region 1 current flows directly downward to Earth on the dawnside and upward on the duskside; the Region 2 current flows directly upward from the Earth on the dawnside and downward on the duskside. In high latitudes, both of these currents will produce large magnetic disturbances, especially in the east and westward components of the B field. Unfortunately, the exact physical formation mechanism of the Region 1 currents is still unclear.

2.5   Ionospheric Currents

According to the theory of divergence-free currents, the field-aligned currents will somehow be closed by currents flowing horizontally in the ionosphere, typically around 100−130 km altitude. Above the F Region (~150 km), E cross B drift makes the electrons and ions drift in the same direction without net current. At middle altitudes, the high collision frequency accelerates ions along the E direction (creating what is known as Pedersen currents, labeled orange in Panel (b) of Figure 1), and the electrons can still continue the E cross B drift (known as Hall currents, labeled red in Panel (b) of Figure 1).

The Solar-quiet (Sq) magnetic field variation supports the existence of the Sq current systems around the low and middle latitudes. The formation of the Sq currents is believed to be relevant to the tidal modes. In addition, due to the difference in solar radiation between the dayside and nightside, the upward polarization E field will significantly strengthen the eastward Hall currents, namely, the EEJ. In the meantime, many studies have detected meridional currents, which connect the two hemispheres. For simplicity, these two current systems, as well as the secondary induced magnetic field due to the time variation of the external currents, will be neglected in this paper.

3.   Coupling of Solar Wind, Magnetosphere, and Ionosphere

As can be seen above, it is almost impossible to observe simultaneously the whole structure, intensity, and evolution of different current systems. In this paper, a numerical coupling model of the solar wind/magnetosphere/ionosphere is used to solve self-consistently the distribution and evolution of the electromagnetic field and particles in the regions of interest. Self-consistent coupling enables MHD to better represent the gradient/curvature drift in the inner magnetosphere and to produce spatial currents that are more realistic.

Here is how it works. By using the measured solar wind (plasma proton number density N, and the velocity V_x) and IMF data (B_y, B_z in Geocentric Solar Magnetospheric (GSM) coordinate system) from the Advanced Composition Explorer (ACE), the Global Magnetospheric (GM) model, BATS-R-US (Block-Adaptive-Tree Solar Wind Roe-Type Upwind Scheme) (De Zeeuw et al., 2004), solves the ideal MHD equations throughout the magnetosphere, which includes a region approximately 32 R_E sunward, 220 R_E tailward, and 126 R_E in each side of the GSM YZ plane, with different spatial resolution in different regions (1/4 R_E inside of the inner magnetosphere). GM then provides the Inner Magnetosphere (IM) with the magnetic field information, average density, and pressure in the flux tubes. IM, which supplies GM with the time-evolving plasma density and pressure on the 2-D spherical grid, was obtained from the Rice Convection Model (RCM), which is shown at the top of Figure 2. Ionospheric Electrodynamics (IE), from the Ridley Ionosphere Model (RIM) (Ridley et al., 2004; Zhang JC et al., 2007), as shown in the bottom of Figure 2, calculates the conductivity and electric field in the ionosphere, driven by solar irradiance and field-aligned currents. The field-aligned currents calculated at 3.5 R_E by GM, which are shown on the left of Figure 2, are provided to IE, and the electric field from IE is passed to GM in the meantime. IE provides IM with electric potential as shown on the right of Figure 2. The date and time are used to update the Earth’s dipole tilt angle throughout the run. The full description of the global coupled MHD-RIM-RCM simulation can be found in the original work of Haiducek et al. (2017).

Figure  2.  Exchange of information among the outer magnetosphere, inner magnetosphere, and ionosphere. The grey-blue at the top and light-blue at the bottom represent the magnetosphere and ionosphere, respectively. A detailed description of the coupling processes is presented in Section 3.

DownLoad: Full-Size Img PowerPoint

4.   Magnetic Perturbations Corresponding to Different Current Systems

Using the numerical simulation described in Section 3, we obtain the three components of the perturbation B field caused by the relevant spatial current systems. Figure 3 shows the global, northern, and southern hemispheric mapping of the three components from top to the bottom, and from left to right: dB_r (positive outward from the center of the Earth), dB_θ (positive from the southern to the northern hemisphere) and dB_ϕ (positive along increasing longitude). The color-bar at the bottom of each panel shows the magnitude of the corresponding component.

Figure  3.  Radial, latitudinal and longitudinal components (from left to right) of perturbation B field due to all the relevant current systems in the magnetosphere and ionosphere. From the top to the bottom are the global, northern, and southern hemispheric mapping of different components of the B field. The color-bar at the bottom of each panel indicates the magnitude of the corresponding component.

DownLoad: Full-Size Img PowerPoint

First, consider the dB_r component in Panel a1 of Figure 3. The most prominent features are the opposite perturbations on the left and the right, which are located on the dayside and nightside, respectively. According to the Faraday law of electromagnetic induction, the positive and negative perturbations on the dayside of the northern (left of Panel b1) and southern (left of Panel c1) hemispheres are the results of the counterclockwise and clockwise magnetopause current, respectively; the negative and positive perturbations on the nightside of the northern (right of Panel b1) and southern (right of Panel c1) hemispheres are the results of the magnetotail magnetopause currents in both hemispheres (black and blue arrows as shown in Figure 1). It is clear that there exist asymmetries between the dayside and nightside, as well as between the southern and northern hemispheres. The perturbation magnitude due to the magnetopause currents ranges from −50 nT to +40 nT.

Next, consider the analysis of dB_θ, presented in the center panels of Figure 3. Significant negative perturbations near the equator appear on the nightside, their magnitude reaching about −160 nT. This disturbance is formed due to the partial ring current, as shown by red arrows in Figure 1. The positive disturbances in polar regions are caused by the Pedersen currents flowing from dawn to dusk. Again, asymmetries between the dayside and nightside, as well as between the southern and northern hemispheres, appear in these two current systems.

Finally, dB_ϕ in Panel a3 exhibits several complex features. Positive perturbation around the duskside at mid-latitude corresponds to the combined effect of the Region 1 current system at high latitude and the Region 2 current system at lower latitude; the negative perturbation corresponds to the Region 1 current system. The dawnside shows features opposite to those of the duskside. The extension of the perturbation to a higher latitude in Panel b3 indicates the azimuthal shift of the field-aligned currents.

Above all, partial ring current plays an important role in the equatorial dB_θ perturbation. Magnetopause currents and tail currents influence the dB_r perturbation around the mid-latitudes. The dB_ϕ and dB_θ perturbations at high latitudes are produced primarily by field-aligned currents and Pedersen currents.

5.   Discussion and Conclusions

Our planet’s intrinsic geomagnetic field makes life possible on Earth. This high-precision geomagnetic field makes our life wonderful. In order to help take full advantage of the low-inclination MSS-1, which is the first high-precision (0.5 nT) geomagnetic measurement scientific satellite, we have briefly reviewed the limited data that have been available to assist in the scientific modeling of external magnetic sources, and thus our understanding of the structures and dynamics of the main current systems in the magnetosphere and ionosphere. Self-consistent coupling of the solar wind, magnetosphere, and ionosphere, for the first time, can soon be used to show quantitively the magnetic perturbation due to comprehensive spatial current systems.

As shown above, partial ring current plays an important role in the equatorial dB_θ perturbation, with a magnitude as high as −160 nT. Magnetopause currents and tail currents influence the dB_r perturbation around mid-latitudes, with perturbation ranging from −50 to 40 nT. Field-aligned currents and Pedersen currents are primary producers of the dB_ϕ and dB_θ perturbations at high latitudes, with magnitudes ranging from −50 to 70 nT. Typical characteristics corresponding to spatial current systems are captured very well by numerical simulation, which will provide new ideas and theoretical support for future physics-based external geomagnetic field modeling. In the near future, it is likely that more accurate magnetic field data with high temporal and spatial resolution, especially the east and westward components provided by MSS-1, combined with the physics-based external field model studied in this paper, will improve significantly our existing geomagnetic field models.

However, the work presented here has significant limitations. First, limited by the inner boundary setting of the numerical simulation, the perturbation B fields shown in this paper are at 3.0 R_E altitude, which is high enough for the height of the geomagnetic measurement satellites (about 450 km for MSS-1). By adopting reasonable modeling methods, it will be possible in the near future to extend the simulation of external magnetic sources to lower altitudes. Second, the Sq, EEJ, and the secondary induced magnetic field perturbation are not included in the present model. The high-precision data provided by MSS-1 will contribute significantly to overcoming these current modeling limitations by making it possible to compare simulations directly to observations.