Modeling of kilometer-scale ionospheric irregularities at Mars

1.   Introduction

The Mars Atmosphere and Volatile EvolutionN (MAVEN) spacecraft were launched in November 2013. One of the orbiter’s objectives is to study the structure of the Martian thermosphere (upper atmosphere) and ionosphere (Jakosky et al., 2015), in particular the poorly understood nightside ionosphere and small scale structure of the planet’s ionosphere. It is well known that ionospheric irregularities in the E and F regions of the terrestrial ionosphere can be observed frequently by remote sensing, in situ measurement, and airglow observation techniques, etc. The scale of Earth’s ionospheric irregularities ranges from sub-meter to hundreds of kilometers (Fejer and Kelley, 1980; Kelley, 2009; Peng YX et al., 2021). The large-scale structure (tens to hundreds of kilometers) of the Martian ionosphere is mainly magnetically controlled by crustal magnetic field sources (Duru et al., 2006; Andrews et al., 2015). However, small-scale ionospheric irregularities of Mars have not been studied sufficiently to reveal their characteristics and physical mechanisms.

Recently, Fowler et al. (2017) reported the first MAVEN observations of small-scale ionospheric irregularities (at scales of 15−20 km or less) in the Martian lower ionosphere. Harada et al. (2018) also report observations by the Mars Advanced Radar for Subsurface and Ionospheric Sounding instrument on the Mars Express of ionospheric irregularities/diffuse echoes. They suggest that gravity waves at Mars might play a significant role in the formation of these ionospheric irregularities. Fowler et al. (2019) have further investigated the characteristics of small-scale ionospheric irregularities. They found that the horizontal magnetic field, the SZA (Solar Zenith Angle) around 75−120 degrees, and outside of the strong crustal magnetic field, might be favorable conditions for small scale ionospheric irregularities. Kilometer-scale ionospheric irregularities were further reported by Fowler et al. (2020). Through a linear model, Keskinen (2018) suggested that the Martian ionosphere in the dynamo region might be unstable due to electromagnetic gradient drift instability. Furthermore, Jiang CH et al. (2021) carried out a nonlinear simulation of ionospheric irregularities, seeded by perturbation zonal winds, in a neutral wind frame (the background zonal wind is set to be zero); their numerical simulations yielded small-scale irregularities (less than the 25 km wavelength of the perturbation wind) but failed to produce smaller-scale (kilometer-scale) variations in electron density and magnetic field profiles comparable to those observed by MAVEN.

The purpose of this study is to reproduce the kilometer-scale variations in electron density and magnetic field profiles. Our nonlinear model assumes a uniform zonal neutral wind (not perturba- tive zonal winds) and the seeding source of ionospheric irregula- rities is chosen to be a cosinusoidal perturbation of the electron density, which could be induced by gravity waves in the Martian thermosphere (Yiğit et al., 2015; Terada et al., 2017). Details of our model and associated assumptions are described in Section 2. Results from the model and analysis are presented in Section 3. Section 4 compares results from our model with results from other simulations and observations. Section 5 summarizes our conclusions.

2.   Model Description

Similar to the model of terrestrial ionospheric irregularities (Jiang CH et al., 2020), Jiang CH et al. (2021) developed a two-dimension nonlinear model to simulate ionospheric irregularities at Mars. In their model, the ion species and neutral species in the Martian dynamo region are, respectively, ${\rm{O}}_{2}^{+}$ and CO_2. Their model solves continuity and momentum equations for ${\rm{O}}_{2}^{+}$ and electrons assuming a divergence-free current and a horizontal background magnetic field. The diamagnetic effect—the sum of magnetic and plasma pressure tends to be constant (Lühr et al., 2003)—was used to calculate the variation of magnetic field. The background electric field was set to be zero, and only the perturbation electric field was considered. In this model, the X, Y, Z directions represent the zonal, meridional, and vertical directions, respectively. A two-dimensional Cartesian (X, Z) grid was applied in this study. The horizontal magnetic field is parallel to the Y direction. The grid consists of 101 points in the zonal direction (X) and 201 points in the vertical direction (Z), with grid spacing of 500 m in the X and 200 m in the Z directions. Periodic boundary conditions were imposed in the X direction. Transmittive boundary conditions were imposed in the Z direction. The running time step is set to 0.01 s in the simulation. Details of the model and numerical schemes are described in Jiang CH et al. (2021).

Unlike the study by Jiang CH et al. , the initial seeding source in this study is a cosinusoidal perturbation of the electron density. England et al. (2017) reported atmospheric gravity waves in the Martian thermosphere with scale sizes in the tens to hundreds of kilometers. Therefore, we set the wavelength of the perturbation in our model at 25 km. MAVEN observations of the Martian ionosphere (Fowler, et al., 2017) have shown that large relative fluctuations (10–50%) in plasma density ($\delta {n_\rm{e}}/{n_\rm{e}}$) and magnetic field ($\delta B/B$) can occur. Therefore, we find it reasonable to set the amplitude of perturbation density to 5% in this simulation when gravity waves occur in the Martian thermosphere (Fritts et al., 2006; Yiğit et al., 2015; Terada et al., 2017; Keskinen, 2018). The background zonal wind is set to be 100 m/s and is kept uniformly horizontal. The initial magnetic field strength is set to be 10 nT. Because ionospheric irregularities are observed to occur primarily at solar zenith angles of ~90−130 degrees, in this model we set the peak ${\rm{O}}_{2}^{+}$ density to be 3 × 10³ cm⁻³ and the corresponding scale height to be 15 km. The background plasma density and magnetic field in this model are comparable to MAVEN observations (Fowler et al., 2017, 2019).

3.   Results

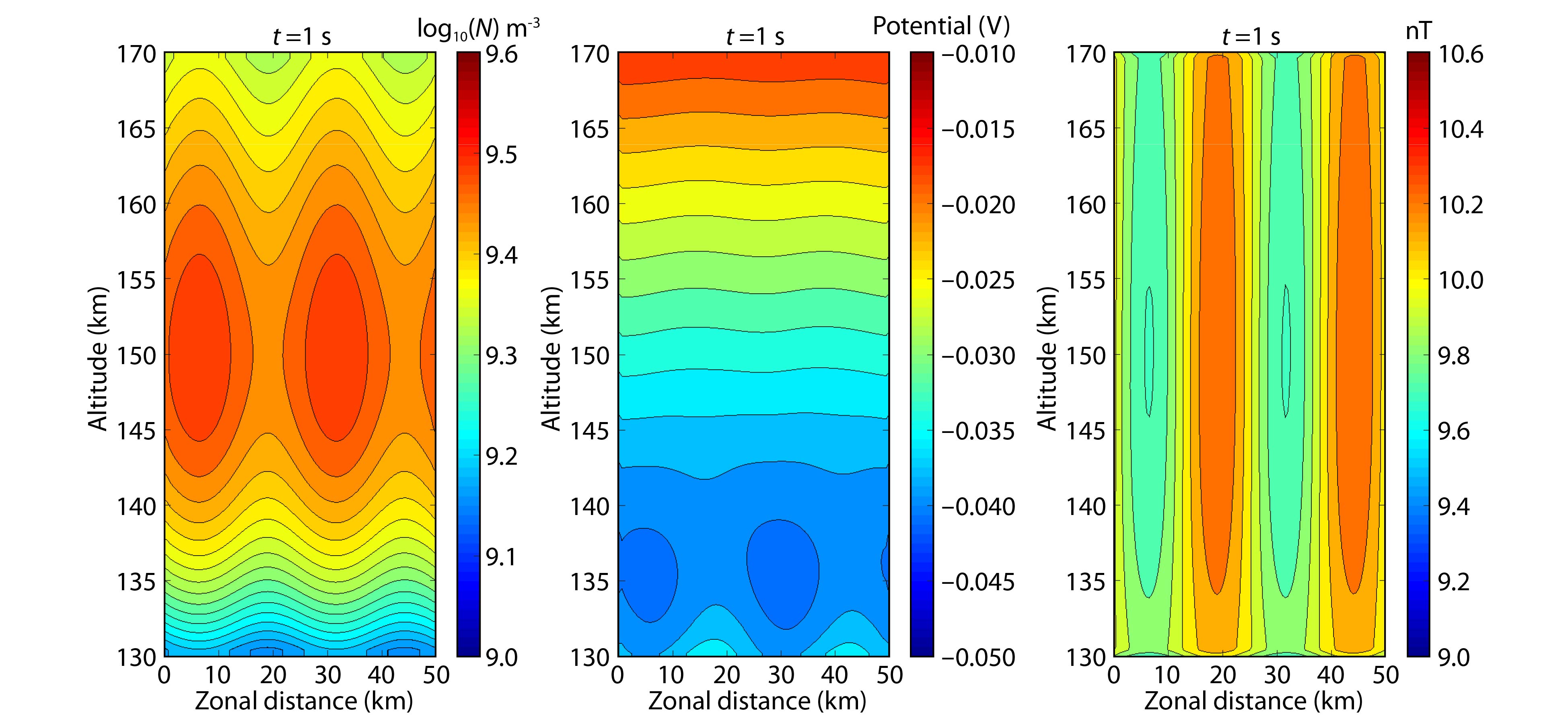
Figure 1 shows the profiles of the plasma density (left panel), electric potential (middle panel), and magnetic field (right panel) at the beginning (t = 1s) of this simulation. The initial plasma density is subject to a cosinusoidal perturbation, which is the seeding source of ionospheric irregularities. Due to the assumption in this model that the sum of magnetic and plasma pressures tends to be constant when the magnetic field is horizontal, the magnetic field fluctuations therefore occur out of phase with the plasma density. It can be seen from Figure 1b that the electric potential fluctuations occur at the beginning stage. The electric potential distribution in the uniform wind is different from that in the previous simulation (Jiang CH et al., 2021). In the Martian ionosphere, the ion-neutral collision is greater than the corresponding gyrofrequency but inverse for electrons. Neutral winds could lead to the separation of the ions and electrons in the dynamo region. Therefore, plasma density fluctuations could plausibly induce a polarization electric field in the Martian ionosphere. We have found that both vertical and zonal electric fields could occur in the plasma density fluctuations. In particular, stronger electric potential perturbations emerge at the bottomside ionosphere due to greater ion-neutral collisions. Obviously, the vertical electric field shear could thus be produced between the bottomside and topside ionosphere. Because the electrons are mostly magnetized in the Martian ionosphere but not the ions, to further demonstrate the distribution of the electric field we have assumed that the posi- tive ions can move away with neutral winds but not the electrons. Accordingly, in the higher plasma density region, more ions will be blown away leaving an excess of electrons. As a result, electrons in the lower plasma density region will be fewer, compared with the higher density region. Furthermore, the potential in the higher density region is lower than in the lower density region. This assumption is consistent with the distribution of the electric potential shown in Figure 1b. However, we should keep in mind that both the plasma density and ion-neutral collisions will play significant roles in determining where the lower potential occurs. Thus, the altitudinal variations of plasma density and ion-neutral collisions could lead to altitudinal variations of electric potential. It also should be noted that the overall electric potential is negative in Figure 1. The negative potential is associated with the effect of the neutral wind. However, the potential difference (the electric field) plays a significant role in the movement of the ${\rm{O}}_{2}^{+}$ ions and electrons in the plasma.

Figure  1.  Plasma density (left), electric potential (middle) and magnetic field (right) distribution simulated at the beginning stage (t = 1 s).

DownLoad: Full-Size Img PowerPoint

Figure 2 shows the nonlinear evolution of the plasma density simulated at t = 0, 100, 300, 500, 700, and 1000 s. It can be seen from Figure 2 that at t = 100 s the lower plasma density moves upward into the higher plasma density region. Due to gradient drift instability in the Martian dynamo region, the zonal electric field induced by plasma density perturbations and neutral winds leads the lower plasma density into higher density regions. After t = 300 s, it is seen clearly that velocity shear of the plasma between the topside and bottomside ionosphere is occurring. The topside plasma moves eastward but the bottomside plasma is moving westward. It also can be seen from Figure 1b that the vertical electric field shear occurs at the altitude of ~135 km. As a result, there are plenty of smaller-scale irregularities in the bottomside ionosphere (see t = 500, 700, and 1000 s in Figure 2). Figure 3 demonstrates the evolution of the associated magnetic field in the present simulation. Similar to Figure 2, plenty of smaller-scale magnetic irregularities can be observed in the bottomside ionosphere (at t = 500, 700, 1000 s). According to the results of the simulation (see Figures 2 and 3), the scale of the irregularity is first associated with the wavelength of the perturbation in the plasma. Then, the most important factor is the velocity shear of the plasma, which leads to Kelvin–Helmholtz instability. At the beginning of the simulation (t = 100 s in Figure 2), the scale of the irregularity corresponds to the wavelength of the perturbation. When the velocity shears of the plasma become stronger in the bottomside of the ionosphere, the scale of the irregularity becomes smaller (see t = 300, 500, 700, 1000 s in Figure 2). In other words, the perturbative electric field is induced by the initial plasma density perturbation; then a Kelvin–Helmholtz instability (caused by the velocity shear of the plasma) leads to smaller-scale irregularity.

Figure  2.  Plasma density distribution simulated at t = 0, 100, 300, 500, 700, and 1000 s.

DownLoad: Full-Size Img PowerPoint

Figure  3.  Similiar to Figure 2 but for magnetic field.

DownLoad: Full-Size Img PowerPoint

Figure 4 shows the variations of electron density and magnetic fields with altitude (Figures 4a and 4b) at the zonal distance of 20 km. The red and blue lines, respectively, represent the running time of 700 and 1000 s. It can be seen from Figure 4 that there are many smaller-scale ‘oscillations’ occurring along the altitude. As the time progresses, smaller-scale perturbations occur at the topside ionosphere (see also Figure 2, at t = 700, 1000 s).

Figure  4.  Vertical profiles of plasma density and magnetic field in this simulation at the zonal distance of 20 km at t = 700 s (red), 1000 s (blue).

DownLoad: Full-Size Img PowerPoint

4.   Discussion

MAVEN observations of small-scale ionospheric irregularities were studied by Fowler et al. (2017, 2019), who reported many smaller-scale (kilometer-scale) ‘oscillations’ along the track of the spacecraft (in both the vertical and horizontal directions). Keskinen (2018) was first to analyze these ionospheric irregularities linearly (both the plasma density and magnetic fluctuations), proposing that the MAVEN observations might be explained by plasma electromagnetic gradient drift instability. Subsequently, Jiang CH et al. (2021) carried out a nonlinear simulation of the Martian ionospheric irregularties in a neutral wind frame (setting the background wind at zero). However, the neutral wind frame simulation did not reproduce the observed altitudinal (vertical direction) kilometer-scale ionospheric irregularities. Fowler et al. (2020) reported that the kilometer-scale ‘oscillations’ structure in the irregularity profiles (vertical direction) can be observed both above and below the ionospheric peak, and pointed out further that two kinds of kilometer-scale irregularities appear in the Martian ionosphere. The density and magnetic field fluctuations vary in and out of phase. In the present simulation, diamagnetic effects are considered. Thus, only out of phase irregularities could be simulated. Figure 4 reveals many kilometer-scale irregularities (out of phase irregularities) reproduced in the profiles of the plasma density and magnetic field, especially below ~155 km. Moreover, the scale of irregularities becomes much smaller around 150−155 km. In the present simulation, the kilometer-scale irregularities in the profiles of the plasma density and magnetic field are comparable to MAVEN observations.

Keskinen (2018) pointed out that the dynamo region of the Martian ionosphere is unstable due to gradient drift instability in the neutral wind. In fact, the growth rates of irregularities in the Martian ionosphere depend on many factors including the neutral wind, the amplitude wavelength of the perturbation in the plasma, the background plasma density, the collision frequency, the magnetic field strength, etc. By calculating the growth rates from the perturbation in the ionospheric plasma density, Keskinen (2018) found that the growth time for irregularities ranged from about 50 to 1000 s for the wavelengths of several kilometers to ~20 km. Figure 4 shows that in our simulation many smaller-scale (kilometer-scale) ‘oscillations’ occur along the altitude at running times of 700 and 1000 s. The growing time of the irregularity in this simulation is consistent with the linear theory proposed by Keskinen (2018). In addition, Keskinen (2018) suggests that the ionosphere is unstable below the ionospheric peak, also pointed out by Fowler et al. (2019). In the present simulation, the ionospheric peak is set at 150 km. However, we found that ionospheric irregularities could reproduced above the ionospheric peak (150 km) at t = 1000 s. In the present simulation, the velocity shear of the plasma (the background neutral wind is set to be uniform) could lead to the Kelvin–Helmholtz instability. Furthermore, the Kelvin–Helmholtz instability produces kilometer-scale plasma density and magnetic irregularities below and above the ionospheric peak. Although the nonlinear model of Martian ionospheric irregularities presented here is simplified by the background parameters of the ionosphere and upper atmosphere, this simplified model can help us understand the nonlinear evolution of ionospheric irregularities at Mars. It is encouraging that these modeling results are comparable to MAVEN observations of kilometer-scale irregularities.

5.   Conclusion

In this study, we carried out a numerical simulation of kilometer-scale irregularities in the Martian ionosphere. A uniform zonal wind was adopted in this model. The seeding source is a cosinusoidal perturbation of plasma density. Modeling results show that the vertical electric field shear can be produced by perturbation of the plasma. The electric field shear in the ionosphere leads to a velocity shear of the plasma between the topside and bottomside ionosphere. Kilometer-scale altitudinal (vertical direction) irregularities are reproduced in the present simulation. Results show that the simulated altitudinal variations of kilometer-scale irregularities in plasma density and magnetic field are comparable to those seen in MAVEN observations.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (NSFC No.42074184 and No.41727804). The numerical code used for this study is not prepared for publicly accessible servers. The data used in this study are available from Zenodo: https://zenodo.org/record/5052664 (DOI: 10.5281/zenodo.5052 664, the section: Numerical Simulation of Small-Scale Ionospheric Irregularities at Mars).